Mathématiques

Cours-TD – Culture Scientifique de base – 2005-2006

Chapitre 5 – Fonctions de plusieurs variables.

Pour ce chapitre, on renoncera à écrire des démonstrations : les bases théoriques, les définitions, sont hors de portée de ce programme. On se contentera donc de décrire les calculs, les règles, en mettant en évidence les similitudes avec les fonctions d’une variable.

1) Généralités

On connaît la notation (x,y) pour un couple de nombres (ou de n’importe quel élément d’un ensemble), paire ordonnée de ces deux éléments. L’ensemble de ces couples se note R². De même R³ est l’ensemble des triplets (x,y,z) de nombres. On peut définir de même R⁴, R⁵, etc., qui correspondent aux ensembles de quadruplets, quintuplés, etc.

Comme les fonctions d’une variable réelle sont des correspondances de R dans R, on peut définir les correspondances de R² dans R, de R³ dans R. Ce sont les fonctions de plusieurs variables.

Exemples : f(x,y,z)=x+y+z la fonction somme de trois variables ; f(x,y)=xy la fonction produit.

On notera une telle fonction comme pour une variable :

f : R³ ® R

(x,y,z) a f(x,y,z)

On peut avoir des problèmes d’ensemble de définition ; par exemple la fonction f(x,y,z)=x/y+y/z+z/x est définie sur l’ensemble des triplets (x,y,z)ÎR³ dont aucun des termes n’est nul.

On a plusieurs interprétations géométriques. D’abord quand on fixe un repère dans le plan ou l’espace, on peut identifier les couples ou les triplets de réels avec les points du plan, ou de l’espace ; on pourrait généraliser, mais il faudrait une théorie des espaces à 4, 5, dimensions. Quoiqu’il en soit, une fonction de plusieurs variables apparaît alors comme une fonction associant un nombre réel à un point du plan ou de l’espace, et on peut même rencontrer des fonctions définies géométriquement.

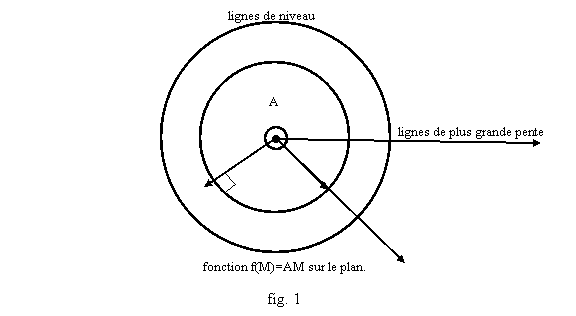
Pour visualiser la façon dont les valeurs de la fonction varie en fonction du point M où on regarde, on peut dessiner – dans le plan pour une fonction de deux variables, ou dans l’espace, pour une fonction de trois variables – les ensembles de points où f(M) garde une valeur constante : ces ensembles s’appellent les courbes de niveau : lignes de niveau (dans le plan) ou surfaces de niveau (dans l’espace). On peut aussi représenter les lignes (dans le plan ou dans l’espace) le long desquelles la variation de f est la plus rapide, qu’on appelle « lignes de plus grandes pentes » : ce sont les courbes en tout point orthogonales aux surfaces de niveau.

Par exemple, si A est un point du plan ou de l’espace, on peut définir f(M)=AM, la distance entre A et M. On a alors, on le rappelle, si les coordonnées (x,y,z) d’un point M sont prises dans un repère orthonormé :

f(M)=, ou en dimension 2.

Ainsi, les lignes de niveau sont les courbes d’équation f(M)=r pour chaque réel r, ce qui correspond au cercle de centre A, de rayon r, dans le plan, ou à la sphère de centre A, de rayon r. Les lignes perpendiculaires à ces lignes de niveau, les « lignes de plus grande pente », sont les demi-droites partant de A (qui portent les rayons des cercles ou sphères : on parle de lignes de niveau radiales). Tout ceci est figuré fig. 1.

Une autre utilisation de la géométrie, est la représentation graphique. Donnons-nous une fonction de deux variables f(x,y). Pour tout couple de point, le triplet (x,y,z) où (x,y) est le couple de point et z=f(x,y), définit un point de l’espace, le point M de coordonnées M(x,y,z). On définit ainsi une surface de l’espace. Pour la représenter, on représente en général le plan P de base, ensemble des points de coordonnées (x,y,0), dirigé par les deux premiers vecteurs de la base, et l’axe des z, dirigé par le troisième vecteur du repère. Au dessus de chaque point (x,y,0) du plan, il y a au plus un point de la surface, le point M(x,y,f(x,y)) si la fonction est définie en (x,y) (fig. 2).

On rappelle que l’équation ax+by+cz=d est une équation de plan dans l’espace. Si c=0, on obtient un plan vertical. Si c¹0, on peut écrire l’équation :

z=ux+vy+w

en divisant par c, et en posant u= -a/c, v= -b/c, w=d/c. Un tel plan est donc la représentation graphique d’une fonction, qu’on appellera aussi affine, si elle s’écrit sous cette forme f(x,y)=ux+vy+w (fig. 3). La direction de ce plan est donnée par le couple (u,v) : les plans parallèles sont ceux qui correspondent au même couple de coefficients. Comme pour les fonction affines, plus u et v sont grands, plus le plan est « penché ». Mais pour retrouver ces coefficients à partir du plan, il faut prendre des points A, A’ correspondant au même y pour obtenir u comme un taux d’accroissement : si A(x,y_A,z) et A’(x’,y_A,z’) sont sur le plan, on a z=ux+vy_A, z’=ux’+vy_A, donc z’-z=[ux’+vy_A]-[ux+vy_A]=u(x’-x), et u=(z’-z)/(x’-x). De même si B(x_B,y,z_B) et B’(x_B,y’,z_B’), ont la même abscisse, on aura v=(z_B’-z_B)/(y’-y). Autrement dit u et v sont des taux d’accroissement de la fonction (x,y) a ux+vy+w, mais u est le taux pris le long des lignes parallèles à (Ox), et v est le taux pris le long des lignes parallèles à (Oy).

Ces repères seront utiles dans la suite. On rappelle en particulier les formules donnant la distance d’un point M(x,y,z) à l’origine du repère (quand celui-ci est orthonormé) :

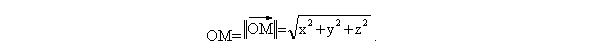
On va maintenant développer des outils permettant le calcul des variations des fonctions de plusieurs variables.

Exercices :

1) Par une étude qualitative, donner l’allure des surface représentant graphiquement les fonctions suivantes :

f(x,y)=0 ; f(x,y)=x+y ;

f(x,y)=(x²+y²)^1/2 (cône de révolution dans un repère orthonormé) ;

f(x,y)=(1-x²)^1/2 (demi-cylindre de révolution) ;

f(x,y)=x²+y² ; f(x,y)=x²-y² ; f(x,y)=sin(x²+y²) ; f(x,y)=x³+y³.

2) Pour les fonctions suivantes, donner l’allure des surfaces (ou des lignes) de niveau et des lignes de plus grande pente, dans l’espace où elles sont définies.

f(x,y,z)=x²+y²+z² ; f(x,y,z)=sin(x²+y²+z²) ; f(x,y)=|x|+|y| ; f(x,y,z)=|x|+|y|+|z| ; f(x,y)=x/y ;

f(x,y)=angle(q) entre la demi-droite [OM) et [Ox), M étant le point de coordonnées (x,y) ;

f(x,y,z)=angle(q) entre [OM) et [Ox) dans le plan (Oxy), M étant le point (x,y,0).

3) eeeeeee

2) Dérivées partielles

Comme on ne sait pas dériver par rapport à une variable double, on prend la même idée que pour les plans : on fixe une des variables, et on calcule localement les variations par rapport à une variable ; si la fonction n’est pas affine, l’analogue de la pente d’une droite, c’est la dérivée.

Définition : soit f une fonction de plusieurs variables (on prend 3 pour simplifier, mais les autres cas se définissent de même), (x₀,y₀,z₀) un triplet de réel. On appelle dérivée partielle de la fonction f en (x₀,y₀,z₀) par rapport à la variable x la dérivée en x₀ de la fonction g de R dans R définie par g(x)=f(x,y₀,z₀). On note ce nombre . On définit de même les dérivées partielles par rapport à y et z.

On n’a donc que des dérivées de fonctions à une variable à calculer, et on peut donc étudier comme pour les fonctions réelles le domaine de dérivabilité. On ne s’occupera pas ici de continuité, car la continuité par rapport à plusieurs variables ne se résume pas à fixer une variable et à faire varier l’autre. Ainsi si f(x,y)=xy/(x²+y²), quand (x,y)¹(0,0), et f(0,0)=0, f(0,y)=f(x,0)=0, mais on ne peut pas dire que « f(x,y) est continue en (0,0) » : ainsi si on regarde le long de la ligne x=y, on aura f(x,x)=x²/(x²+x²)=x²/(2x²)=1/2, ne tend pas vers 0.

On supposera donc toujours que les fonctions sont « suffisamment continues ». Et même, en général, que les dérivées partielles elles-mêmes sont « suffisamment continues ».

On parlera quand même de fonctions qui tendent vers 0 quand elles dépendent de la distance OM, ce qui entraîne que, quelle que soit la droite, la valeur de f deviendra petite. Par exemple f(M)=OM, la distance OM elle-même, qui tend vers 0 quand M tend vers l’origine O, ou f(M)=OM², f(M)=1-cos(OM), etc.

Le calcul des dérivées partielles obéit aux mêmes règles que les dérivées de fonctions d’une variable pour ce qui est du calcul de dérivées d’un produit, d’une somme, d’un quotient, de la composée gof d’une fonction f de plusieurs variables par une fonction g de R dans R.

Exemples :

f(x,y)=ux+vy+w affine ; on calcule les dérivées partielles en supposant que y est constant, par exemple, et en dérivant par rapport à x : on trouve u car vy, w ne dépendent pas de x donc sont « constants » – de dérivée 0 – quand on fixe y, et ux est une fonction linéaire en x, de dérivée u, donc la dérivée partielle est u+0+0=u. De même on peut dériver par rapport à y, on trouve :

 ; .

f(x,y,z)=xyz. Alors quand on fixe y et z, le coefficient yz doit être vu comme une constante, et f comme la fonction linéaire x a (yz)x, dont la dérivée est yz. On fait de même pour les autres variables :

 ;  ; .

f(x,y,z)=e^x2+y2+z2 ; la dérivée de l’exponentielle est la fonction elle-même, donc par composition on trouve :

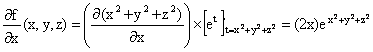 ; et de même :

 ; .

Dernier exemple : f(x,y,z)=x/y+y/x. Cette fonction est définie quand x et y sont non nuls, et elle est alors dérivable :  ; . En effet pour dériver par rapport à x, la partie x/y s’écrit x(1/y), c’est une fonction linéaire de x, et la partie y/x=(1/x)y se dérive comme 1/x, puisque y doit être pris comme constant.

On a une interprétation similaire à celle du développement limité à l’ordre 1 : les dérivées partielles donnent les coefficients de la fonction affine qui approche « le mieux possible » la fonction f, au sens que la différence avec f(x,y) sera plus petite que toute somme affine en x,y,z, ou, ce qui suffit, négligeable devant |x|+|y|+|z|, ou devant toute somme dont on peut vérifier qu’elle est équivalente comme la norme de OM, . Comme en dimension 2, les fonctions (x,y,z) a ux+vy+wz+p sont les fonctions affines de 3 variables. On a ainsi :

Propriété : si f est une fonction suffisamment régulière, dérivable par rapport à toute les variable en (x₀,y₀,z₀), alors la fonction :

D : (x,y,z) a f(x₀,y₀,z₀)+(x-x₀)+(y-y₀)+(z-z₀)

est le développement limité (ou application tangente) de f en (x₀,y₀,z₀) à l’ordre 1, on peut écrire :

f(x,y,z)=D(x,y,z)+(|x|+|y|+|z|)N(|x|+|y|+|z|),

où N est une fonction de R₊ dans R qui tend vers 0 en 0.

La fonction L(X,Y,Z)=X+Y+Z s’appelle partie linéaire du développement, qui s’écrit donc D(x,y,z)=f(x₀,y₀,z₀)+L(x-x_0, y-y₀, z-z₀).

Le vecteur Ñf(x₀,y₀,z₀)=i+j+k, si i,j,k sont les vecteurs de base, s’appelle gradient de f en (x₀,y₀,z₀). D’après les formules de calculs, le nombre (x-x₀)+(y-y₀)+(z-z₀) n’est autre que le produit scalaire de Ñf(x₀,y₀,z₀) avec le vecteur M₀M entre M₀(x₀,y₀,z₀) et le point variable M(x,y,z).

L’application L se nomme aussi différentielle de f au point (x₀,y₀,z₀), et se note df_(x0,y0,z0).

On note ainsi dx, dy, dz les différentielles des fonctions coordonnées. Or elles sont facilement calculables :

Regardons pour la fonction « première coordonnée », (x,y,z) a x : en un point (x₀,y₀,z₀), les dérivées partielles de cette fonction sont, par rapport à x,y et z, 1, 0 et 0. La différentielle dx_(x0,y0,z0) est donc toujours la même fonction linéaire, la fonction coordonnée elle-même.

De même dy_(x0,y0,z0) est toujours la fonction deuxième coordonnée (y), et dy_(x0,y0,z0) est la fonction troisième coordonnée (z). Du coup on résume tout ceci sous la forme suivante : pour une fonction f ayant des dérivées partielles en (x₀,y₀,z₀), on aura pour tout (X,Y,Z) :

df_(x0,y0,z0)(X,Y,Z)=X+Y+Z

=dx_(x0,y0,z0)(X,Y,Z)+dy_(x0,y0,z0)(X,Y,Z)+dz_(x0,y0,z0)(X,Y,Z)

ce qu’on résume par la formule :

df =dx+dy+dz.

On rencontre souvent cette formule en science expérimentale, traduite pour un triplet (X,Y,Z) « petit » et pour exprimer que l’application différentielle est une bonne approximation de la variation de f entre (x₀,y₀,z₀) et un point voisin.

Quand on veut mettre en évidence qu’on regarde les variation de f entre deux points voisins, on utilise pour une variable une lettre comme h et on regarde par exemple f(a+h)-f(a) au lieu de f(y)-f(x) avec y,x quelconques ; pour plusieurs variables on fait de même. Par exemple l’approximation de f par la différentielle s’écrira :

f(x₀+h,y₀+k,z₀+l)=f(x₀,y₀,z₀)+df_(x0,y0,z0)(h,k,l)+(|h|+|k|+|l|)e(h,k,l)

=f(x₀,y₀,z₀)+h+k+l+(|h|+|k|+|l|)e(h,k,l)

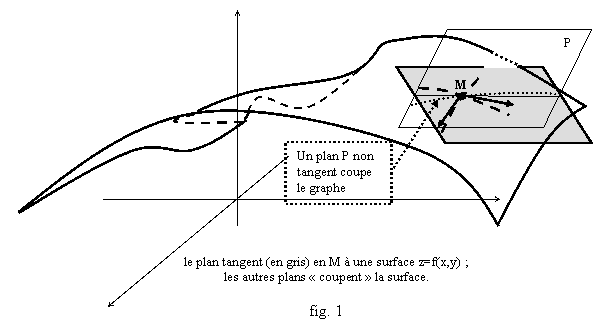
Interprétation géométrique : quand on est en deux variables, l’application tangente D(x,y) définit un plan z=D(x,y), qui est le plan tangent au graphe de f (fig. 1).

Ce plan est bien le plan qui approche « le mieux » la surface qui est le graphe de f.

L’intérêt des dérivations n’est pas ici de déterminer les monotonies des fonctions, car cette notion n’a aucun sens. En effet, il n’y a pas d’ordre possible entre les points du plan ou de l’espace, en tout cas pas d’ordre « total » qui fixerait automatiquement, pour deux points A et B, lequel est plus petit ou plus grand. Donc définir la « croissance » d’une fonction n’a pas de sens. Une fonction f(x,y) peut croître quand x croît mais décroître quand y décroît.

Néanmoins on a quand même un approchant du théorème des accroissements finis :

Inégalité des accroissements finis : Soit f une fonction dérivable sur toute une zone de l’espace. En tout point (x,y,z) de cette zone, on suppose que la norme 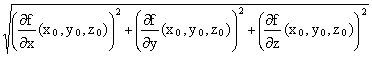du vecteur Ñf est plus petite que le même nombre k positif. Alors on pour tout couple de point A,B dans la zone :

|f(B)-f(A)|£k´AB.

Autre interprétation géométrique : lignes de pente, ligne de niveau et gradient.

Si on écrit le développement limité d’une fonction à l’ordre 1, écrit avec la notation gradient, on obtient :

Or un produit scalaire est nul si les vecteurs sont orthogonaux. Par ailleurs le produit scalaire nul signifie que le développement limité est égal à f(M₀), donc que f(M)-f(M₀) est négligeable devant les fonctions affines. Autrement dit que M se déplace sur une ligne où f reste constante ou varie peu : la ligne de niveau de M₀.

1^ère propriété : le gradient est orthogonal aux lignes de niveau.

Par ailleurs si M est dans la direction du gradient, le produit scalaire sera maximum : le produit scalaire c’est le produit des normes des vecteurs par le cosinus de leur angle, c’est donc quand l’angle est nul et le cosinus égal à 1 que le produit est maximum : à une même distance de M₀, c’est le long de la ligne orientée suivant Ñf que f(M) augmente le plus, et c’est le long de cette ligne, mais dans le sens contraire, que f(M) diminue le plus puisque cela correspond à un angle de p avec Ñf et un cosinus de -1.

2^ème propriété : les lignes de plus grandes pentes, le long desquelles la variation de f est la plus rapide, sont en tout point dirigées par le gradient.

(C’est-à-dire que le gradient leur est tangent. Elles sont orthogonales aux lignes de niveau, et f(M) est croissant le long de ces lignes, quand on va dans le sens du gradient.)

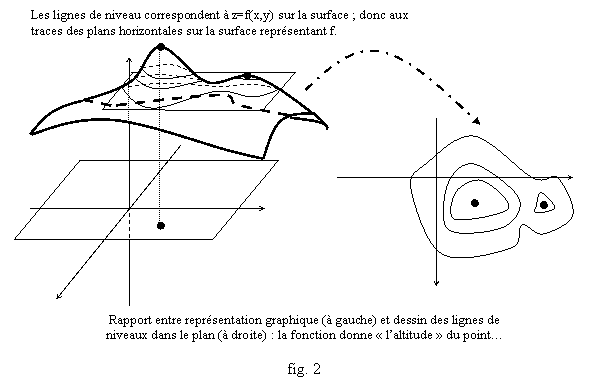
Tout cela, ce sont des remarques qualitatives. Une représentations utile est la suivante : soit f une fonction du plan dans R, interprétons la comme une fonction « altitude » : le graphe représente alors un paysage, les lignes de plus grandes pentes et les lignes de niveau ont le sens géométrique courant, et quand on le regarde de haut, on voit le plan – « la carte du paysage », avec les lignes de niveau, les gradients, etc. (fig. 2).

Dans l’espace, la même idée est applicable : on peut y dessiner les surfaces de niveaux, les lignes (orthogonales à ces surfaces) qui marquent le chemin où la fonction augmente « le plus vite », mais on peine à comparer au graphe d’une telle fonction, car ce graphe a besoin d’un espace de dimension 3+1=4 pour être représenté… En revanche, on peut penser à une fonction donnant la température ou la pression en fonction du point où on se trouve : les surfaces de niveaux sont alors les isothermes ou les isobares, de telles représentations sont courantes dans les cartes météorologiques…

Exemple de calcul de plans tangents : les sphères.

La demie sphère supérieure de centre O et de rayon 1 est l’ensemble des points de coordonnées (x,y,z) tels que z³0 et x²+y²+z²=1. Ces conditions s’écrivent z=. La demi-sphère est donc le graphe de la fonction définie sur le plan par f(x,y)=. Soit un point de coordonnées (x₀,y₀) où f est défini, et M₀(x₀,y₀,z₀) le point du graphe correspondant, tel que z₀=f(x₀,y₀). Alors , donc le plan tangent a pour équation z= ou encore zz₀=-xx₀-yy₀+x₀²+y₀²+z₀², c’est-à-dire :

xx₀+yy₀+zz₀=1 (compte tenu de x₀²+y₀²+z₀²=1).

Finalement l’équation s’écrit en terme de produit scalaire (en supposant toujours qu’on est dans un repère orthonormé) : un point M est sur le plan si et seulement si :

soit, compte tenu de la relation

La condition est donc que (MM₀) soit perpendiculaire à la droite (OM) : L’ensemble des points M est le plan passant par M₀, perpendiculaire au rayon (OM₀) (fig. 3).

Exercices :

1) Calculer les dérivées partielles des fonctions suivantes, en précisant en quels points elles sont définies :

f(x,y)=|x-y|^1/2 ; f(x,y)=xy ; f(x,y,z)=xyz ; f(x,y,z)=(x+1)(y²+1)(z³+3) ;

f(x,y)=e^x+y ; f(x,y,z)=(x²+y²+z²)^1/2 ; f(x,y,z)=x/y+y/z+z/x.

2) dddddddd

3) Formules de Taylor, application aux recherches d’extrema

Si une fonction de plusieurs variables est dérivable par rapport à toutes ces variables, on peut chercher à dériver ses dérivées partielles. On définit :

Définition : une fonction f(x,y) est deux fois dérivable si elle est dérivable et si les dérivées par rapport à x ou y sont dérivables par rapport aux deux variables.

Appelons f’_x, f’_y les dérivées par rapport à x et y. On obtient donc 4 fonctions en dérivant à nouveau, pour lesquelles on introduit des notations :

(f’_x)’_x=f’’_x²=, (f’_x)’_y=f’’_xy=,

(f’_y)’_x=f’’_yx=, (f’_y)’_y=f’’_y²=

La formule suivante est valable dans la plupart des cas :

Propriété (formule de Schwarz) : si f est « suffisamment régulière » (en pratique : par exemple si elle admet des dérivées partielles d’ordre 2 continues) et deux fois dérivable en un point (x,y) par rapport à x puis à y, elle l’est par rapport à y puis à x, et on a l’égalité :

On peut aussi calculer des dérivées supérieures, définir les fonctions 3 fois, 4 fois, etc. – ou indéfiniment - dérivables.

On se contente ici de donner la formule de Taylor à l’ordre 2, raffinant le « DL » déjà donné à l’ordre 1 :

Si f est deux fois dérivable en un point (x₀,y₀), on peut écrire :

f(x,y)=f(x₀,y₀)

+(x-x₀)+(y-y₀)

+(1/2)[(x-x₀)²+(y-y₀)²+2(x-x₀)(y-y₀)]

+(|x-x₀|+|y-y₀|)²d(x,y)

avec d(x,y) ® 0 quand (x,y) ® (x₀,y₀).

Ou encore :

f(x₀+h,y₀+k)=f(x₀,y₀)

+h+k

+(1/2)[h²+k²+2hk]

+(|h|+|k|)²e(h,k)

avec e(h,k) ® 0 quand (h,k) ® (0,0).

Cette formule se généralise pour les fonctions à trois, quatre variables. Le terme d’ordre 2 sera toujours (1/2) fois la somme des carrés plus la somme des produits (« rectangles »).

Trois variables : le terme d’ordre 2 dans la formule de Taylor développant

f(x+h,y+k,z+l)-f(x,y,z)

s’écrit :

(1/2)[h²+k²+l²+2hk+2kl+2lh]

n variables : le terme d’ordre 2 dans la formule de Taylor développant

f(x₁+h₁,x₂+h₂,…,x_n+h_n)-f(x₁,x₂,…,x_n)

s’écrit :

(1/2)[+2]

Utilisation de la formule de Taylor : le problème de l’extremum

Un extremum local est défini de la même manière que pour une fonction de la variable réelle. Précisément :

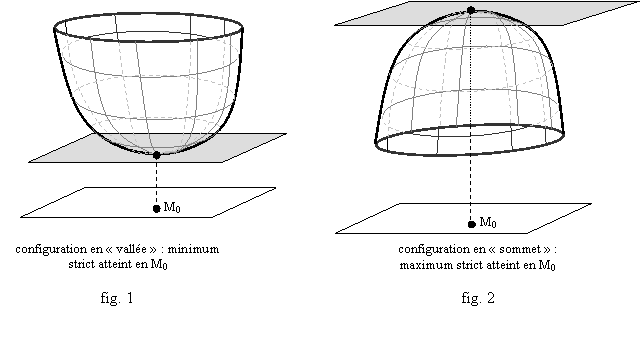
Définition : Une fonction f définie sur l’espace (respectivement : sur le plan) présente un maximum local strict au point M₀, si on peut trouver une boule B (respectivement : un disque D) de centre M₀, et de rayon R>0, tel que, pour tout point M de B (respectivement : de D) différent de M₀, on ait : f(M)<f(M₀) (fig. 1).

On définit bien entendu maximum absolu, maximum (au sens large), minimum, etc. Si la fonction f présente un extremum local en M₀, alors les dérivées partielles sont nulles en ce point.

Propriété : Soit f une fonction définie sur R³. Si f présente un extremum local en (x₀,y₀,z₀), et est dérivable en ce point, alors les dérivées partielles en (x₀,y₀,z₀) sont nulles (et donc le plan tangent en ce point est parallèle au plan (Oxy), c’est-à-dire horizontal).

Preuve : supposons qu’il s’agisse, par exemple, d’un maximum local. On peut trouver une boule B de centre M₀(x₀,y₀,z₀) et de rayon r>0 sur lequel, pour tout point M(x,y,z), on ait :

f(x,y,z)£f(x₀,y₀,z₀).

Alors soit un point M de coordonnées (x,y₀,z₀). La distance MM₀ est proportionnelle à |x-x₀|. Il s’ensuit que pour tout xÎ]x₀-kr,x₀+kr[, on a MÎB. Donc :

f(x,y₀,z₀)£f(x₀,y₀,z₀) si xÎ]x₀-r,x₀+r[.

Ceci signifie que la fonction g définie par g(x)=f(x,y₀,z₀) a un maximum local en x₀. Comme cette fonction est dérivable en x₀ par hypothèse, on a forcément g’(x₀)=0, c’est-à-dire, puisque c’est la définition de la dérivée partielle :

=0.

On prouve de la même façon que : ==0.

Remarque :

Pour prouver que les dérivées partielles sont nulles, on s’est contenté d’étudier la variation de f(x,y,z) le long de trois droite passant par (x₀,y₀,z₀), les parallèles aux axes de coordonnées. Mais il y a une infinité de droite passant par M₀(x₀,y₀,z₀), et il est possible d’avoir des dérivées partielles nulles, et même un maximum le long de ces droites, mais pas de maximum quand on regarde dans d’autres directions. On va voir des exemples de ce fait, encore plus aisés à obtenir que pour les fonctions d’une variable (ou la dérivée peut s’annuler sans qu’on ait de maximum). Autrement dit, avoir un extremum entraîne avoir des dérivées partielles nulles, mais le contraire n’est pas du tout vrai.

Définition : on appelle point critique d’une fonction f de plusieurs variables un point où toutes les dérivées partielles sont nulles, c’est-à-dire où la différentielle est nulle.

Etude des valeurs de f deux fois dérivable autour d’un point critique.

1^er cas : fonction d’une variable.

C’est un cas déjà étudié, mais il illustre bien la démarche qu’on aura pour 2 variables ou plus.

On a donc f’(x₀)=0, et donc un DL₂(x₀) de la forme suivante :

f(x₀+h)=f(x₀)+0h+(1/2)f’’(x₀)h²+h²e(h)=f(x₀)+h²(A+e(h)).

où e(h) tend vers 0 quand h tend vers 0.

On a posé A=(1/2)f’’(x₀). Si A est non nul, le terme en facteur de h² tend vers A, et est donc du signe de A dans un (petit) intervalle ]-r,r[ (ce qui correspond à x₀+h dans un « petit » intervalle ]x₀-r,x₀+r[).

Si A>0, on a donc un intervalle ]-r,r[ où :

h²(A+e(h))>0 quand h¹0,

c’est-à-dire :

f(x₀+h)-f(x₀)>0 ou encore f(x₀+h)>f(x₀) :

on a donc un minimum local strict.

Si A<0, on a donc un intervalle ]-r,r[ où :

h²(A+e(h))<0 quand h¹0,

c’est-à-dire :

f(x₀+h)-f(x₀)<0 ou encore f(x₀+h)<f(x₀) :

on a donc un maximum local strict.

Si A=0, le terme carré se réduit à h²e(h) et donc il faudrait pousser le développement plus loin pour conclure (c’est le cas de la fonction x a x³ en x₀=0).

Soit f une fonction de deux variables, pour simplifier, et deux fois dérivable en M₀(x₀,y₀). On suppose que M₀ est un point critique, mais que toutes les dérivées partielles d’ordre 2 ne sont pas nulles en (x₀,y₀), et on applique la formule de Taylor :

2^ème cas : fonction de deux variables.

On a vu que le développement de Taylor à l’ordre 2 s’écrit :

f(x₀+h,y₀+k)=f(x₀,y₀)

+h+k

+(1/2)[h²+k²+2hk]

+(|h|+|k|)²e(h,k)

avec e(h,k) ® 0 quand (h,k) ® (0,0).

Si (x₀,y₀) est un point critique, le développement se réduit à :

f(x₀+h,y₀+k)=f(x₀,y₀)+(1/2)[ah²+ck²+bhk]+(|h|+|k|)²e(h,k)

en posant : a= ; b=2 ; c=.

On peut, de la même façon que pour le cas d’une variable, vérifier que le signe de f(x₀+h,y₀+k)-f(x₀,y₀) ne dépend que du signe de ah²+ck²+bhk quand il est non nul, pour (h,k) dans une (« petite ») boule de centre (0,0) et de rayon r>0.

Or on peut écrire si a¹0 : ah²+ck²+bhk=a[h²+(b/a)hk+(c/a)k²]

=a[(h+(b/2a)k)²+((4ac-b²)/(4a²)]k²]

=a[(h+(b/2a)k)²-[D/(4a²)]k²]

Si D<0, on a une somme de deux carrés, toujours strictement positive sauf si h+(b/2a)k=k=0, ce qui équivaut à h=k=0, donc l’expression ah²+ck²+bhk est du signe strict de a (et de c car b²-4ac<0 n’est possible que si a et c sont non nuls et de même signe), sauf en (0,0).

Si a,c>0, on aura donc f(x₀+h,y₀+k)-f(x₀,y₀)>0 pour (h,k) assez petit et (h,k)(0,0), ce qui s’écrit :

f(x₀+h,y₀+k)>f(x₀,y₀)

On a donc un minimum local strict en (x₀,y₀) (configuration en vallée : fig. 1).

Si a,c<0, on aura donc f(x₀+h,y₀+k)-f(x₀,y₀)<0 pour (h,k) assez petit et (h,k)(0,0), ce qui s’écrit :

f(x₀+h,y₀+k)<f(x₀,y₀)

On a donc un maximum local strict en (x₀,y₀) (configuration en « sommet » : fig. 2).

Si D>0, on a une différence de deux carrés.

Si h+(b/2a)k=0, ce qui équivaut à h=-(b/2a)k, c’est-à-dire le long d’une droite, l’expression ah²+ck²+bhk s’écrit -a[D/(4a²)]k², et est du signe strict de -a, sauf en (0,0).

Si k=0, c’est-à-dire le long d’une autre droite, parallèle à l’axe (Ox), l’expression ah²+ck²+bhk s’écrit ah², et est du signe strict de a, sauf en (0,0).

Ainsi on trouve des points (x₀+h,y₀+k) aussi voisins qu’on veut de (x₀,y₀) pour lesquels :

f(x₀+h,y₀+k)-f(x₀,y₀)>0 et f(x₀+h,y₀+k)>f(x₀,y₀),

et d’autres pour lesquels :

f(x₀+h,y₀+k)-f(x₀,y₀)<0 et f(x₀+h,y₀+k)<f(x₀,y₀).

On est donc sûr que f n’a ni minimum ni maximum local en (x₀,y₀) (configuration en « selle de cheval » : fig. 3)

Si D=0, l’expression se réduit à : a(h+(b/2a)k)².

Le long de la droite h= -(b/2a)k, l’expression ah²+ck²+bhk est nulle. Ce qui signifie que le signe de

f(x₀+h,y₀+k)-f(x₀,y₀)=f(x₀-(b/2a)k,y₀+k)-f(x₀,y₀)

ne dépend que du terme (|h|+|k|)²e(h,k) et donc il faudrait pousser plus loin le développement et on obtiendrait, dans la plupart des cas, des termes d’ordre 3 quand (h,k) varie dans la direction que la droite h= -(b/2a)k. Au total, quitte à changer les axes, l’allure de la courbe au voisinage de (x₀,y₀) ressemble à l’allure de la surface représentant la fonction (x,y) a x²+y³ en (0,0) (configuration en « bec de canard », fig. 4).

(néanmoins, dans certains cas, même en allant à l’ordre supérieur, on peut trouver un extremum ou encore une allure similaire au cas D>0. Exemples en fig. 5.)

Remarque : on n’a pas traité le cas a=0. Si c¹0, on peut échanger les rôles de a et c et la discussion est la même. Si a=c=0, soit b=0 dans ce cas le terme d’ordre 2 est nul, on ne peut rien dire, on peut obtenir des configurations beaucoup plus compliquées. Si b¹0, on est dans le cas D=b²-4ac=b²>0, et même si l’expression ah²+ck²+bhk se réduit à bhk, on peut remarquer que hk s’exprime quand même sous la forme :

(1/4)[(h+k)²-(h-k)²]

comme différence de carrés, donc on est dans le même cas que dans la discussion ci-dessus (« selle de cheval »).

3^ème cas : fonctions de trois variables ou plus.

Dans tous les cas, une expression « homogène de degré 2 » (combinaison de termes h_i² et de produits h_ih_j), va pouvoir se décomposer en somme de carrés parfait. On doit donc opérer cette transformation, et si on trouve n termes pour n variables, avec des coefficients de même signe, on a bien un extremum. Sinon on n’a pas d’extremum (termes avec des signes différents) ou un cas ambigu (moins de n termes, coefficients de même signes, donc une somme de carrés pour certaines coordonnées, et des termes manquants, qui seraient en fait d’ordre 3, 4, etc., pour les autres coordonnées).

Exemples :

Signe de : A(h,k,l)=h²+k²+l²+hk+kl+lh ?

On peut écrire :

h²+k²+l²+hk+kl+lh=h²+h(k+l)+k²+l²+kl

=[h+(k+l)/2]²-(1/4)(k+l)²+k²+l²+kl

=[h+(k+l)/2]²-(1/4)(k²+l²+2kl)+k²+l²+kl

=[h+(k+l)/2]²+(3/4)k²+(3/4)l²+(1/2)kl

=[h+(k+l)/2]²+(3/4)k²+(3/4)l²+(1/2)kl

=[h+(k+l)/2]²+(3/4)[k²+(2/3)kl+l²]

=[h+(k+l)/2]²+(3/4)[(k+(1/3)l)²-(1/9)l²+l²]

=[h+(k+l)/2]²+(3/4)(k+(1/3)l)²+(2/3)l²

A(h,k,l) se décompose en somme de trois carrés, donc A(h,k,l)>0, sauf si h+(k+l)/2=k+(1/3)l=l=0, ce qui revient à dire h=k=l=0.

Signe de : B(h,k,l)=hk+kl+lh ?

On peut écrire :

hk+kl+lh=hk+l(h+k)

=(h+l)(k+l)-l²

=(1/4)[[(h+l)+(k+l)]²-[(h+l)-(k+l)]²]-l²

=(1/4)[h+k+2l]²-(1/4)[h-k]²-l².

L’expression n’a donc pas de signe constant sur R³ (carrés avec des coefficients différents ; ainsi A(h,h,0)=h²>0 si h¹0, et A(h,-h,0)=-h²<0 si h¹0).

4) Appendices : autres propriétés sur les fonctions de plusieurs variables et l’utilisation du calcul différentiel dans un cadre géométrique

A- Une dernière formule : changement de variables

Une formule plus compliquée de composition des fonctions correspond à un « changement de variables » :

Propriété : Soit f(u,v,w) une fonction de trois variable, dérivable au point (u₀,v₀,w₀), et on suppose donnée u(x,y,z), v(x,y,z), w(x,y,z) des fonctions dérivables par rapport à x en (x₀,y₀,z₀), triplet tel que u(x₀,y₀,z₀)=u₀, v(x₀,y₀,z₀)=v₀, w(x₀,y₀,z₀)=w₀. Alors la fonction g(x,y,z) définie par :

g(x,y,z)=f(u(x,y,z),v(x,y,z),w(x,y,z))

est dérivable par rapport à x en (x₀,y₀,z₀) et on a :

formule qu’on résume par :

Cette formule est adaptable quand on dérive par rapport aux autres variables, ou n’a qu’une ou deux variables u,v à la place des trois u,v,w, et aussi quand on n’a qu’une ou deux variables x,y, à la place des trois x,y,z. Ainsi si f est une fonction de deux variables f(u,v), et que u,v sont exprimés en fonction d’une variable x, on aura :

A titre d’exemple on va vérifier ceci quand on a deux variables à chaque fois, f(u,v) et u(x,y), v(x,y). On considère donc g(x,y)=f(u(x,y),v(x,y)) et on cherche si g est dérivable par rapport à x en (x₀,y₀). On a donc à étudier :

[g(x,y₀)-g(x₀,y₀)]/(x-x₀)=[f(u(x,y₀),v(x,y₀))-f(u(x₀,y₀),v(x₀,y₀))]/(x-x₀)

=[f(u(x,y₀),v(x,y₀))-f(u(x₀,y₀),v(x,y₀))+f(u(x₀,y₀),v(x,y₀))-f(u(x₀,y₀),v(x₀,y₀))]/(x-x₀)

=[f(u(x,y₀),v(x,y₀))-f(u(x₀,y₀),v(x,y₀))]/(x-x₀)+[f(u(x₀,y₀),v(x,y₀))-f(u(x₀,y₀),v(x₀,y₀))]/(x-x₀)

=[(u-u₀)/(x-x₀)][f(u(x,y₀),v(x,y₀))-f(u(x₀,y₀),v(x,y₀))]/(u-u₀)

+[(v-v₀)/(x-x₀)][f(u(x₀,y₀),v(x,y₀))-f(u(x₀,y₀),v(x₀,y₀))]/(v-v₀)

et chacune de ces deux sommes tendra, si on a les « bonnes » propriétés de continuité, vers les expressions voulues, respectivement et .

Un exemple :

Un changement de variable : les coordonnées polaires.

On se donne une fonction f(x,y) et on veut repérer les points par leur coordonnées polaires, (r,t). On a alors x=r cos(t) et y=r sin(t), donc :

, et :

.

B- Courbe paramétrées

On a parlé dans les descriptions qualitatives des fonctions de plusieurs variables de « lignes de niveau », de « lignes de plus grande pente ». Le concept « symétrique » de fonctions de plusieurs variables, à savoir : une seule variable, plusieurs fonctions (qui seront des coordonnées), permet de définir les courbes paramétrées. C’est un concept entrevu au A-, puisqu’on a parlé de plusieurs fonctions variant en fonction des mêmes variables, pouvant être réduites à une.

Définition : on appelle courbe paramétrée dans le plan (resp. dans l’espace) une fonction de R dans le plan (resp. l’espace), t a M(t). Si on a fixé un repère, cela revient à se donner 2, ou respectivement 3, fonctions coordonnées t a x(t) et t a y(t) (resp. t a z(t)).

Si on voit une courbe comme la « trajectoire » d’un point, concept usuel de la cinématique, le vecteur :

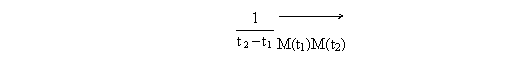
est la vitesse moyenne entre les instant t₁ et t₂, et sa limite quand t₁=t est fixe et que t² ® t, est le vecteur vitesse, appelé plus généralement vecteur dérivée de la courbe, de coordonnées (x’(t), y’(t)) (resp. (x’(t),y’(t),z’(t))).

L’étude des variations simultanées des deux (ou trois coordonnées) permet de dessiner la courbe. Quand on dit que la ligne de plus grande pente est sans cesse tangente au gradient d’une fonction de deux (ou trois variables), cela signifie qu’on peut la décrire comme une courbe paramétrée dont le vecteur dérivé soit sans cesse colinéaire au gradient.

On peut aussi définir une courbe par une équation implicite :

f(x,y)=0 dans le plan.

Une telle équation peut se traduire en équation paramétrée. Le plus simple est souvent d’exprimer y en fonction de x ou x en fonction de y en « résolvant l’équation » en x ou en y.

Quand on est dans l’espace, une équation implicite f(x,y,z)=0 définit une surface, et l’intersection de deux surfaces peut définir une courbe.

C- extrema liés

On a vu au paragraphe 3 comment trouver les extrema d’une fonction de deux ou trois variables.

Un problème classique est de chercher les extrema de fonctions de trois variables, f(x,y,z), quand le point M(x,y,z) est sur une surface donnée (plan, sphère). Si la surface est le graphe d’une fonction de deux variables (u,v) a g(u,v), il suffit d’étudier les extrema de la fonction (u,v) a f(u,v,g(u,v)), ce qui est un problème déjà étudié.

En revanche si la surface est définie par une équation implicite : h(x,y,z)=0, le problème est différemment posé.

Mais en fait on a une propriété qui prépare une recherche similaire à celle des « points critiques » : Les extrema sont des points (x,y,z) où les gradients Ñf et Ñh sont colinéaires.