Mathématiques

Cours-TD – Culture Scientifique de base – 2005-2006

Chapitre 4 – Etudes de fonctions.

1) Pratique des études de fonctions

On va maintenant récapituler comment étudier une fonction donnée, pour pouvoir tracer son graphe, résoudre les équations dans lesquelles elle est impliquée.

Ensemble de définition

Soit f une fonction. La première tâche est de déterminer son ensemble de définition D_f, en cherchant avec précision sur quels intervalles elle est définie, par exemple pour quelles valeurs de x, si la fonction est donnée par une formule de calcul, on peut effectuer les opérations.

Une fois déterminé D_f, il convient de l’écrire comme réunion, finie ou infinie, d’intervalles. En effet tous les théorèmes usuels, tant sur la dérivation que sur la continuité, ne s’appliquent que sur des intervalles. Il faut d’ailleurs, à cette étape, déterminer où la fonction est continue et dérivable. En outre, aux bornes des intervalles composant D_f, on peut avoir à prouver que f est prolongeable par continuité, c’est-à-dire a une limite finie, et peut être remplacée par la fonction égale à f sur D_f et à la limite en ce point. Il arrive qu’un tel prolongement soit dérivable, voire indéfiniment dérivable.

Symétries de la courbe et intervalles d’étude

Ensuite, on étudie les symétries de la fonction. Si f est paire ou impaire, tout ce qu’on dit sur le comportement de f sur R₊ donne le comportement de f sur R_-, par la transformation (x,f(x))a(-x,f(x)) si f est paire, ou (x,f(x))a(-x,-f(x)) si f est impair. Pour le graphe cela correspond aux symétries axiale d’axe (Oy) et centrale de centre O. Mais il y a d’autres symétries possibles.

La symétrie, pour le graphe, d’axe la droite (x=a), est la transformation (x,y)a(2a-x,y). Le graphe est donc invariant par cette symétrie si on a toujours f(x)=f(2a-x). Ce qui veut dire que si pour un réel b on a f(x)=f(b-x) pour tout x, alors il suffit de faire l’étude pour les x³a=b/2 (fig. 1).

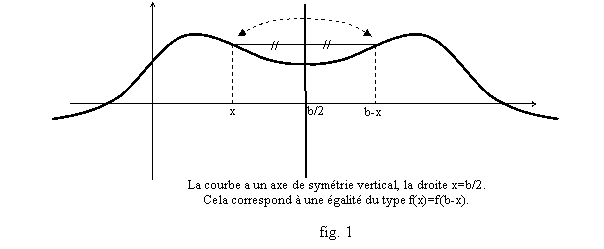
De même la symétrie de centre A(a,z) s’écrit (x,y)a(2a-x,2z-y). Autrement dit s’il y a deux réels b,c tels que pour tout x, f(b-x)=c-f(x), alors la courbe est symétrique par rapport au point (a,z) avec a=b/2, z=c/2, et il suffit de faire l’étude pour x³a (fig. 2).

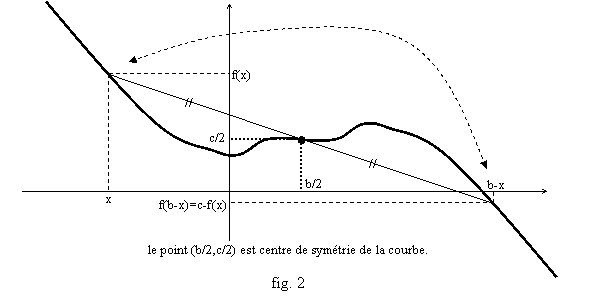
Une autre forme de symétrie concerne les fonctions périodiques : f est périodique de période T si pour tout x on a f(x+T)=f(x). Cela signifie que si le point (x,y)=(x,f(x)) est sur la courbe, alors le point (x+T,y)=(x+T,f(x)) l’est aussi. Autrement dit la translation de vecteur (T,0) laisse invariante la courbe et il suffit de faire l’étude de la fonction sur un intervalle de longueur T, comme [0,T] ou [-T/2,T/2].

En fait la courbe sera invariante par translation du vecteur de composantes (U,V) si on a f(x+U)=f(x)+V pour tout x. C’est le cas par exemple de la fonction f(x)=x+sin(x), puisque f(x+2p)=(x+2p)+sin(x+2p)=x+sin(x)+2p=f(x)+2p. On a ici U=V=2p (fig. 3).

Dans tous les cas il suffit de faire l’étude sur un intervalle de longueur U, puisque la translation ne changera pas le sens de variation, etc.

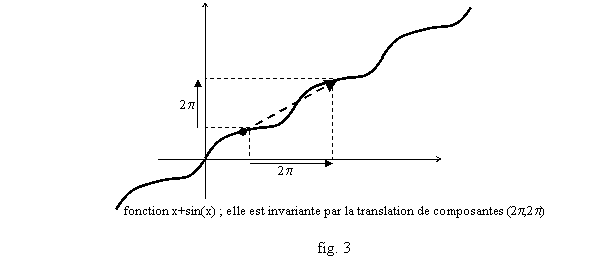
Ces remarques permettent souvent de raccourcir considérablement les études de fonctions. Néanmoins quand on utilise ou recherches de telles « symétries », il faut prendre garde au domaine de définition. On n’a pas mentionné cet aspect pour alléger l’exposé, mais cet au détriment d’une certaine rigueur. Par exemple, pour vérifier qu’une fonction est paire, il ne faut se contenter de vérifier que f(x)=f(-x) quand x et -x sont dans D_f ; il faut aussi vérifier que, pour tout x où f est définie, f est aussi définie en -x. Pour vérifier que f est périodique de période T, il faut aussi vérifier que pour tout x tel que f(x) soit défini, f(x+T) est aussi défini. Dans la pratique, on rencontre souvent des fonctions définies partout. Mais ce n’est pas automatique, par exemple la fonction tangente est périodique de période, elle est définie sur R privé des nombres de la forme p/2+kp, pour tous les entiers kÎZ. Donc si tan(x) est défini, x n’est pas de la forme p/2+kp, x+p ne le sera pas non plus et tan(x+p) sera défini.

De toute manière il faut déterminer, sur D_f, un sous-ensemble, décomposé en intervalles, sur lequel on va faire l’étude.

Variations de la fonction, signe de la dérivée

Ensuite on cherche le sens de variation de la fonction.

Si c’est possible, on peut déterminer le sens de variation sans dériver la fonction : par exemple une somme de fonctions croissantes est croissante, un produit de fonctions croissantes positives est une fonction croissante. Bien souvent on s’épargne de longs calculs ainsi, et on peut, au moins sur certains intervalles, trancher facilement.

Sinon, on calcule f’(x) et on cherche le signe de f’(x), par exemple en résolvant l’inéquation f’(x)>0. Il arrive que cela ne soit pas facile. On essaie alors d’isoler une partie de l’expression dont dépend le signe de f’(x). Par exemple si f(x) est un quotient, le dénominateur dans f’(x) est un carré toujours positif, et on étudie le numérateur isolément. De toute façon pour déterminer le signe de f’(x) ou d’une partie qui lui confère le signe, il se peut qu’on doive de nouveau dériver. On met alors plusieurs lignes dans le tableau de variation, donnant les variations de f’(x) sur la première ligne, en déduisant les endroits où f’(x) change de signe sur la deuxième, etc.

Exemple : si f(x)=e^x-x², f’(x)=e^x-2x n’a pas un signe facile à cerner. On calcule f’’(x)=e^x-2. Donc f’’(x) est positive pour x>ln(2), négative pour x<ln(2). Donc f’(x) est croissante pour x>ln(2), décroissante pour x<ln(2), et a donc un minimum absolu sur R en ln(2). En ce point on a f’(ln(2))=e^ln(2)-2.ln(2)=2-2ln(2)=2(1-ln(2))>0 car e>2 donc 1>ln(2). Il s’ensuit que f’(x) est toujours >0, donc f est strictement croissante.

On voit que c’est l’étape qui peut nécessiter un certain nombre de calculs. Une fois trouvées les variations de f, on fait le tableau de variation.

Tableau de variations

On fait un tableau où, sur l’horizontal, on peut lire les valeurs de x variant dans l’intervalle de d’étude. On met sur la première ligne les valeurs de x « critiques » : limites des intervalles d’études, points où f ’(x) change de signe, qu’on peut d’ailleurs rajouter au fur et à mesure de la confection du tableau, valeurs où f(x) n’est pas défini. Sous chacune de ces valeurs on porte des lignes verticales dans le tableau.

Ensuite on met les lignes qui servent à étudier le signe de f’ : seulement f’(x) si le signe est facilement trouvé, ou f’’(x), f’’’(x), etc., s’il faut aller jusque-là. On met les lignes en portant entre les traits verticaux les informations connues : signes ou sens de variation (matérialisées par des flèches signifiant « strictement croissant, strictement décroissant, constant ») et en utilisant les informations portées sur chaque ligne pour remplir la ligne suivante.

Enfin, une fois bien connu le signe de f’(x), on met les sens de variation de f dans la dernière ligne, en précisant bien les valeurs prises par f aux points où il y a des minima ou maxima locaux. Il convient aussi de préciser le comportement de f aux valeurs critiques, notamment les limites aux points où f n’est pas définie. En ces points il faut aussi, s’il y a une limite finie, préciser si la courbe a une tangente, autrement dit si on peut aussi prolonger f’(x). On rappelle que si f’(x) a une limite en un tel point à gauche ou à droite, cela donne une valeur de la dérivée à gauche ou à droite ou, si la limite est infinie, une demi-tangente verticale. On rappelle aussi que si f’(x) n’a pas de limite, il peut y avoir une tangente quand même (exemple : x²sin(1/x)).

Pour ces calculs de limites, on doit parfois utiliser des développements limités. De toute manière, on ne les entreprend que si cela semble indispensable, ou demandé explicitement.

De toute manière il faut porter les valeurs limites dans le tableau, sur la ligne donnant les variations de f. Ainsi une flèche allant vers le haut entre les barres correspondant à x=0 et x=1, avec en bas de la flèche –¥ et en haut 2, signifiera « la fonction est strictement croissante sur ]0,1], tendant vers –¥ en 0⁺ et valant 2 en 1 ».

Ainsi le tableau de variation doit donner entièrement les intervalles où f est croissante, décroissante, et sur chaque intervalle où elle est strictement monotone, les valeurs portées en haut des flèches doivent donner l’image de l’intervalle. Jusqu’aux limites en ±∞ si elles existent.

En ces endroits où x ou f(x) tendent vers l’infini, on développe des descriptions plus précises des allures possibles de la courbe : c’est l’étude des « branches infinies », expliquée au paragraphe 2.

Exemple 1 : Etudier la fonction f(x)=sin(x)+1/sin(x).

1^ère étape : sinus étant de classe C^∞, f est indéfiniment dérivable là où elle est définie, c’est-à-dire quand sin(x)¹0. Autrement dit quand x n’est pas un multiple de p. Ainsi D_f est la réunion des intervalles ]kp, (k+1)p[ entre deux multiples de p.

2^ème étape : symétries de la courbe. La fonction sinus étant 2p périodique, f l’est aussi (sous-entendu : son domaine de définition aussi est stable quand on remplace x par x+2p, x-2p, etc.). Par ailleurs f est impaire (comme le sinus) : si sin(x)¹0, alors sin(-x)= -sin(x)¹0 et :

f(-x)=sin(-x)+1/sin(-x)= -sin(x)+1/(-sin(x))= -sin(x)-1/sin(x)= -f(x).

Il suffit donc de faire l’étude sur ]0,p[, pour en déduire le graphe sur ]-p,0[ (symétrie de centre O origine du repère) et donc sur R (périodicité).

On peut même faire mieux : comme sin(p-x)=sin(x) pour tout x, on aura aussi f(p-x)=f(x), ce qui signifie que la courbe est symétrique par rapport à la droite verticale d’équation x=p/2.

En fin de compte il suffit de garder comme intervalle d’étude : ]0,p/2].

3^ème étape : étude sur l’intervalle choisi. On peut calculer :

f’(x)=cos(x)+(-sin’(x))/sin²(x)=cos(x)-cos(x)/sin²(x)=cos(x)(sin²(x)-1)/sin²(x).

Comme le sinus est entre 0 et 1 strictement sur ]0,p/2[, ainsi que cos(x), on a sin²(x)-1<0 et sin²(x)>0, cos(x)>0 sur cet intervalle donc finalement f’(x)<0 sur ]0,p/2[ (f’(p/2)=0 mais cela n’influence pas le sens de variation sur ]0,p/2] ; cela exprime juste que f présentera un minimum en p/2, ce qui est logique vu l’axe de symétrie de la courbe).

F est donc strictement décroissante sur ]0,p/2]. Enfin f(p/2)=sin(p/2)+1/sin(p/2)=1+1/1=2, et quand x tend vers 0 en restant positif, sin(x) tend vers 0 en restant positif donc 1/sin(x) tend vers +∞ et f(x) aussi. On peut donc tracer le tableau de variation de f :

Et on peut donc tracer le graphe de f (fig. 4), en utilisant les symétries pour le compléter (on pouvait aussi les utiliser pour compléter le tableau sur un domaine plus grand).

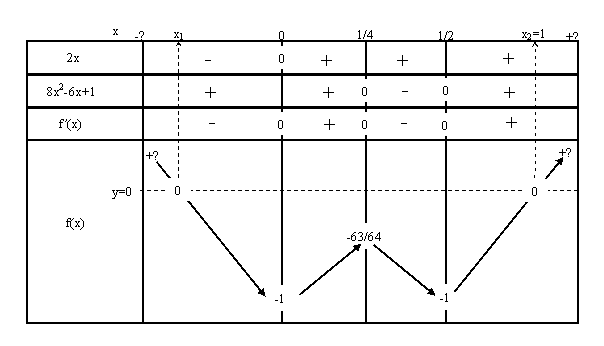
Exemple 2 : Etudier sur R la fonction f(x)=4x⁴-4x³+x²-1. Que peut-on dire de l’équation f(x)=0 ?

La fonction f est définie partout, continue, dérivable. Il n’y a pas de symétries évidentes. Dans ce cas on n’en cherche pas, ce serait plus long que le temps gagné à étudier f sur R tout entier.

Calculons f’ :

f’(x)=4(4x³)-4(3x²)+2x=16x³-12x²+2x.

Pour trouver le signe de f’, il faut résoudre l’équation f’(x)=0 qui n’est pas vraiment de degré 3 car 2x est en facteur :

f’(x)=2x(8x²-6x+1).

Donc les solutions de f’(x)=0 sont 0, et les solutions de 8x²-6x+1=0. Pour cette équation on a D=(-6)²-4´8´1=36-32=4=22. On a donc deux racines, [6-2]/16=1/4, et [6+2]/16=1/2 ; de plus 8x²-6x+1 est négatif entre ces nombres, et positif ailleurs. On a donc le tableau de signe de f’ et le tableau de variation de f, en calculant les valeurs aux extrema locaux de f :

f(0)=4´0⁴-4´0³+0²-1= -1 ;

f(1/4)=4/4⁴-4/4³+1/4²-1=(1/4-1+1)/4²-1=1/4³-1=-63/64 ;

f(1/2)=4/2⁴-4/2³+1/2²-1=1/4-1/2+1/4-1= -1.

Par ailleurs en ±∞ c’est le terme x⁴ qui est prépondérant : f(x)=4x⁴(1-1/x+1/(4x²)-1/(4x⁴)), donc si x tend vers ±∞, les termes en 1/x, 1/x², 1/x⁴ tendent vers 0, donc la parenthèse tend vers 1-0+0-0=1, et comme 4x⁴ tend vers +∞ (aussi bien en +∞ qu’en -∞), f(x) tend vers +∞.

Muni de ces renseignements on peut donner le tableau de f. Il y apparaît que l’équation f(x)=0 a deux solutions, une, x₁, sur ]- ∞,0[ et l’autre, x₂, sur ]1/2,+∞[. Pour cette deuxième, comme 1 est racine évidente (f(1)=4´1⁴-4´1³+1²-1=4-4+1-1=0), on connaît sa valeur. Le tableau semblant symétrique par rapport à x=1/4, il est logique de penser que, si x₂=1 est racine, alors l’autre racine doit être x=2(1/4)-1= -1/2 : effectivement on a x₁= -1/2 car :

f(-1/2)=4(-1/2)⁴-4(-1/2)³+(-1/2)²+1= 4/2⁴-(- 4/2³)+1/2²-1= 4/16+4/8+1/4-1=1/4+1/2+1/4-1=0.

Pour voir si cette impression de symétrie est justifiée, il faut comparer, pour un réel x quelconque, les nombres f(2(1/4)-x)=f(1/2-x) et f(x). Or, comme on peut écrire :

f(x)=4x⁴-4x³+x²-1=x²(4x²-4x+1)-1=x²(2x-1)²-1,

on aura :

f(1/2-x)=(1/2-x)²[2(1/2-x)-1]²-1

=(1/2-x)²(1-2x-1)²-1

=(1/2-x)²(2x)²-1

=(1/2-x)²(2²)(x²)-1

=[2(1/2-x)]²x²-1

=(1-2x)²x²-1

=(2x-1)²x²-1

=f(x)

ce qui prouve que la droite d’équation x=1/4 est bien un axe de symétrie pour la courbe.

Mais dans ce cas, il n’est pas évident qu’on aurait gagné du temps à la chercher au départ (c’est-à-dire qu’on aurait mis moins de temps pour trouver cet axe et conclure qu’il suffisait d’étudier f sur ]-∞,1/4] ou [1/4,+∞[, qu’on en a mis pour étudier le signe de f’ et les variations de f sur R tout entier).

En tout cas on peut maintenant, pour tracer la courbe de f (fig. 5), commencer par tracer l’axe de symétrie, puis tracer la portion de la courbe correspondant par exemple à x £1/4, et compléter par symétrie.

Enfin, pour se donner une idée de la direction de la courbe en certain points particulier, on peut calculer f’. Ainsi en x₁= -1/2 où f(x₁)=0, on a :

f’(-1/2)=16(-1/2)³-12(-1/2)²+2(-1/2)= -16/8-12/4-1= -2-3-1= -6.

Remarque : quand x ® ±∞, comme on a dit que c’est le terme en 4x⁴ qui était prépondérant dans f(x), on se doute que l’allure de la courbe sera similaire à celle de y=4x⁴ (comme une parabole, mais qui monte plus rapidement). On dit que la courbe présente une branche parabolique verticale tournée vers les y positifs, notion qui sera définie au paragraphe 2 (définition vérifiée par f).

Exercices

1) Etudier les fonctions f suivantes, et en déduire le nombre de solutions de l’équation f(x)=0, et un encadrement entre des entiers – ou plus précis si possible – de ces solutions, en illustrant ces études par une représentation graphique : f(x)=x³-x²+3x+1 ; f(x)=x³-4x²+3x+1 ; f(x)=x³-3x²+3x+1 ; f(x)=x³-4x²+3x-11 ; f(x)=x⁴-3x²+2x-1.

2) Mêmes questions ; on ne cherchera pas forcément à avoir des valeurs exactes des minima et des maxima locaux des fonctions : f(x)=x⁴-2x²-1 ; f(x)=x⁴-2x²-3x-1 ; f(x)=x⁵-5x³+10x-2 ; f(x)=4x⁵-5x⁴-20x³+30x²-7.

3) Faire l’étude complète des fonctions suivantes, et illustrer cette étude par une représentation graphique : f(x)=e^x-x³ ; f(x)=e^x-x⁴ ; f(x)= ; f(x)=x^x+1/x ; f(x)=(x+1/x)^x ; f(x)=x^sin(x).

4) On pose f(x)=x/ln(x) ; étudier et représenter la fonction f. Utiliser cette étude pour discuter le nombre de solutions de l’équation : a^x=x^a, en fonction de la valeur de a>0.

5) Etudier et représenter les fonctions suivantes :  ;  ;  ; f(x)=x-tan(x).

2) Etudes de branches infinies

On se place dans la situation suivante : on a mené à bien l’étude d’une fonction f, comme décrit dans le paragraphe 1. Mais, à certaines zones de son domaines de définition, f(x) devient infini, ou c’est x qui peut tendre vers ±¥ (ou bien ce sont les deux : x tend vers ±¥ et f(x) aussi). Dans ce cas, il faut étudier ces « branches infinies », pour tracer plus facilement la courbe : ce qu’on veut savoir, c’est, par exemple, s’il y a une droite D telle que, pour certaines valeurs de x, le point (x,f(x)) se rapproche de la droite tout en ayant une de ses coordonnées qui tend vers l’infini. On fait en général cette étude juste après avoir dressé le tableau de variation de la fonction, et juste avant de dessiner la courbe.

1^ère branche infinie : asymptote verticale

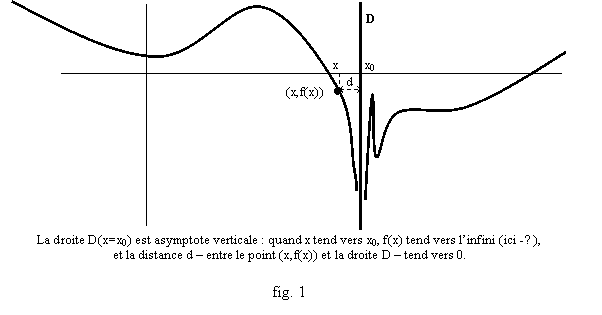
Le plus simple est le cas où x reste borné, tendant vers une valeur « limite » x₀ de D_f, et donc c’est f(x) qui tend vers ±¥, et la droite D doit être la droite verticale d’équation x=x₀ (fig. 1).

Définition : Si, en une valeur x₀, on a f(x) qui tend vers +¥ ou -¥ à gauche ou à droite en x₀, on dit que la droite verticale D d’équation x=x₀ est une asymptote de la courbe de f.

Quand x tend vers x₀, la distance du point (x,f(x)) à la droite est donc |x- x₀| (puisque le point (x₀,f(x)) est sur D), qui tend vers 0 mais le point ne rejoint jamais la droite, puisque on a x>x₀ ou x<x₀, et ne s’en rapproche qu’ « à l’infini ». C’est cela que désigne le mot d’ « asymptote ».

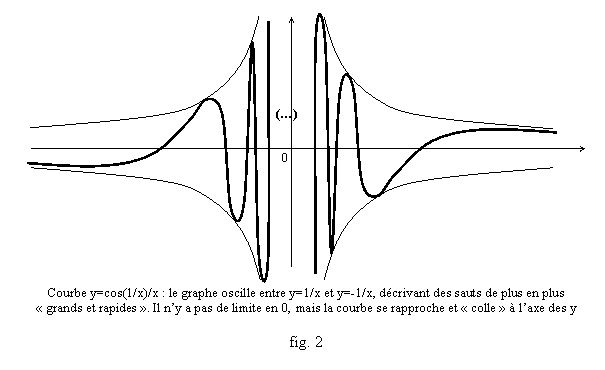
Notons qu’on a exclu arbitrairement de la définition les cas comme f(x)=cos(1/x)/x où f(x) se rapproche sans cesse de l’axe verticale x=0, mais en prenant des valeurs parfois positives et parfois négatives, donc sans tendre ni vers +¥ ni vers -¥ (fig. 2). En fait on ne considère pas qu’il s’agit là d’une asymptote mais un tel comportement mérite néanmoins qu’on le signale lors d’une étude de fonction.

2^ème cas : droite asymptote en ±¥

Enfin le cas le plus varié est celui où x tend vers ±¥. On prendra +¥ dans la description mais le cas x®-¥ se décrit de la même manière.

Le cas le plus simple est que le point (x,f(x)) se rapproche d’une droite D donnée (fig. 3). L’équation de D doit être de la forme y=ax+b, car D ne peut être verticale (sinon x ne pourrait tendre vers +¥ et le point (x,f(x)) se rapprocher de D en même temps, les droites verticales correspondant à x=constante).

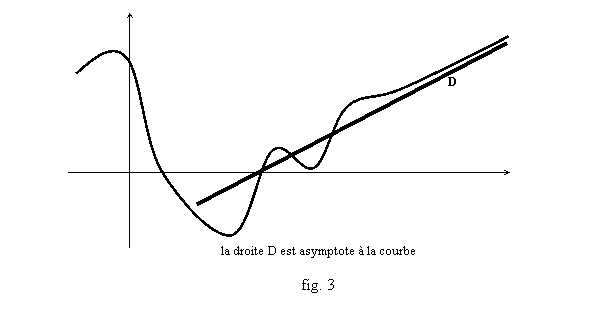
Quand le repère est orthonormé, la distance d’un point M(x₀,y₀) à une droite D d’équation ux+vy+w=0 est donnée par d=|ux₀+vy₀+w|/(u²+v²)^1/2 (formule connue ou admise). Ainsi la distance du point (x,f(x)) à la droite D d’équation y=ax+b, est donnée par |f(x)-ax-b|/(1+a²)^1/2. Ainsi la distance tend vers 0 si et seulement si f(x)-ax-b tend vers 0 en +¥. Cela donne d’ailleurs un point de D très proche de chaque point (x,f(x)) de la courbe, à savoir le point (x,ax+b).

Quel que soit le repère, dire que f(x)-ax-b tend vers 0 signifiera que le point de la courbe M(x,f(x)) d’abscisse x est de plus en plus proche du point (x,ax+b) de D qui a la même abscisse, puisque la différence de leurs ordonnées tend vers 0. C’est bien l’idée d’une droite « de plus en plus proche » de la courbe.

Enfin notons qu’une telle asymptote est unique : si f(x)-ax-b et f(x)-a’x-b’ tendent tous deux vers 0, leur différence aussi. Or elle vaut :

[f(x)-ax-b]-[f(x)-a’x-b’]=(a’-a)x+(b’-b).

Si x tend vers +¥, (a’-a)x tend vers +¥ ou –¥ sauf si a’=a. Si la limite est nulle, on doit avoir a’=a. la différence se réduit alors à la constante b’-b, qui doit être égale à la limite, soit b’-b=0.

On a donc prouvé l’unicité.

Définition : On dit que la courbe de f présente une asymptote quand x tend vers +¥, égale à la droite d’équation y=ax+b, si f(x)-ax-b tend vers 0 quand x tend vers +¥. Cette droite est alors unique. On a la même définition en -¥. Plus généralement on dira que les courbes de deux fonctions f(x) et g(x) sont asymptotes en +¥ si f(x)-g(x) tend vers 0 quand x tend vers +¥. De même en -¥.

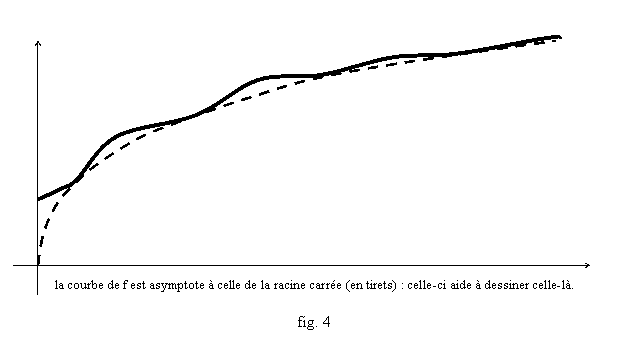
Cette notion de « courbes asymptotes » ne sera pas vraiment utilisée cette année. Néanmoins, dans certains cas particulier, on peut la mentionner. Par exemple si g(x) est une fonction simple, dont la courbe est très connue, on pourra s’en aider pour représenter le graphe de f. Ainsi définissons, sur R₊, f(x)= ; on remarque que f(x)³ donc f(x) tend vers +∞ quand x tend vers +∞, et, en utilisant la quantité conjuguée, on remarque que :

.

Donc la courbe de f(x) est asymptote à la courbe de la racine carrée (fig. 4).

Sur la piste des asymptotes : les directions asymptotiques

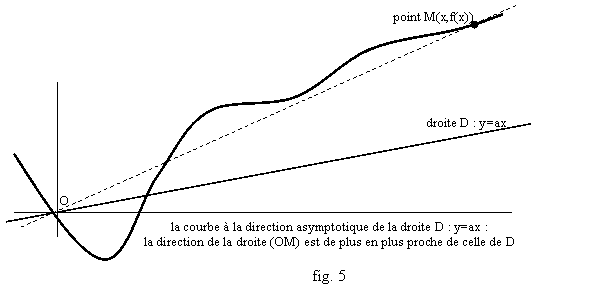
Comment trouver l’asymptote à partir du calcul de f ? Le terme prépondérant parmi ax+b est ax car ax+b=ax[1+b/(ax)] et que b/(ax) tend vers 0 dons est négligeable devant 1 quand x est assez grand. Donc si f(x) est « très proche » de ax+b, f(x) doit augmenter « à peu près » comme ax quand x augmente. On peut le voir en regardant la limite de f(x)/x. Si f(x)-ax-b tend vers 0 quand x tend vers +¥, cela tend aussi vers 0 quand on le divise par x. Or cela donne f(x)/x-a-b/x, avec b/x qui tend vers 0. Donc f(x)/x tend vers a. On pose donc la définition générale suivante.

Définition : On dit que f(x) a la direction asymptotique de la droite y=ax en +¥ si f(x)/x tend vers a quand x tend vers +¥ (fig. 5). On a la même définition en -¥.

Sur la piste des asymptotes : asymptotes et branches paraboliques

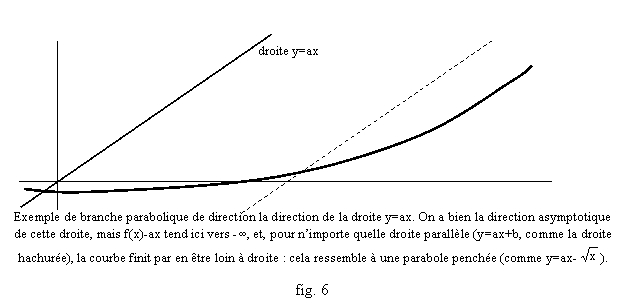
Ainsi on commence par calculer cette limite, et si on la trouve égale à a, on cherche la limite de f(x)-ax. Dans ce cas si c’est un réel b, on a une asymptote. Si en revanche c’est +¥ ou -¥, la courbe croît comme ax, c’est-à-dire que si x augmente de X, f(x) augmente environ de aX, mais en s’éloignant de toute droite y=ax+b, en étant toujours de plus en plus loin au dessus, ou au dessous. On donne donc une définition générale décrivant ce phénomène, qui est celui des courbes du type y=x^1/2 qui sont des paraboles :

Définition : On dit que la courbe de f a une branche parabolique de même direction que la droite y=ax si f(x)/x tend vers a et si f(x)-ax tend vers +¥ ou tend vers –¥ quand x tend vers +¥ (fig. 6).

Enfin, quand on a la direction asymptotique de y=ax, mais que f(x)-ax n’a pas de limite, la courbe suivra « grosso modo » la direction de y=ax mais sans pouvoir décrire plus précisément son comportement. Par exemple f(x)=x+sin(x) s’enroule autour de la droite y=x, qui donne sa direction asymptotique, mais n’a pas d’asymptote, car f(x)-x passe sans cesse de -1 à 1. Ce graphe a été esquissé au paragraphe 1, fig. 3.

Directions asymptotiques : le cas a=0

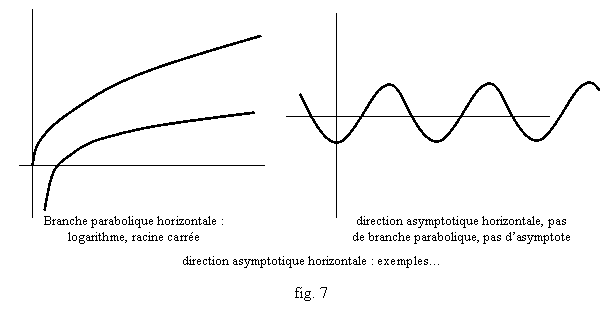
Mentionnons d’ailleurs que si a=0, c’est-à-dire que f(x)/x tend vers 0, on parle bien sûr de direction asymptotique de l’axe (Ox), et les exemples de courbes ayant cette direction asymptotique mais avec une branche parabolique ou même sans que f(x)-ax=f(x) ait de limite, sont plus familiers et « plus parlants ». C’est le cas de f(x)=ln(x), ou f(x)=, qui ont des branches paraboliques en direction de (Ox), ce qui permet de bien visualiser cette allure (fig. 7), et quand f(x)=sin(x) (ou cos(x)), la fonction a bien la direction asymptotique horizontale, mais ne s’approche d’aucune droite en particulier, puisqu’elle oscille, « s’enroule », sans cesse autour de l’axe (Ox) (fig. 7).

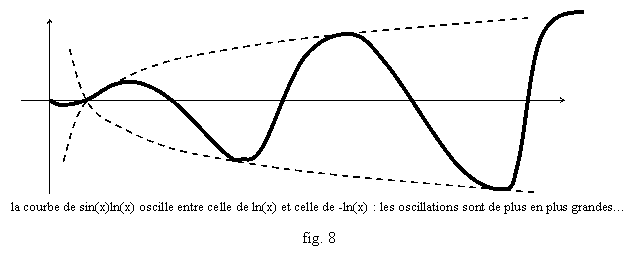
Mais, comme l’imagination ne connaît pas de limite, on peut toujours faire « pire » : regardons par exemple f(x)=sin(x)ln(x). Comme |f(x)|£|ln(x)| on aura |f(x)/x|£|ln(x)|/x®0 et donc f(x)/x tend vers 0 quand x tend vers +∞. Mais la courbe, oscillant entre les courbes y=ln(x) et y= -ln(x), au fur et à mesure que sin(x) oscille entre 1 et -1, a une allure pour le moins déroutante, et dans un tel cas l’information qu’on a une direction asymptotique a une valeur plus limitée que dans les cas des branches paraboliques ou des asymptotes (fig. 8).

Enfin, quand on a une direction asymptotique horizontale, avoir une asymptote signifie que la différence f(x)-ax=f(x)-0x=f(x) (puisque a=0) tend vers un réel b : autrement dit, quand f(x) a une limite b si x tend vers +∞, c’est que la droite d’équation y=b est asymptote. C’est une notion familière, et dans ce cas aussi les dessins semblent souvent « plus parlants » pour mettre en évidence le fait que f(x) se rapproche de la droite y=b (fig. 9)

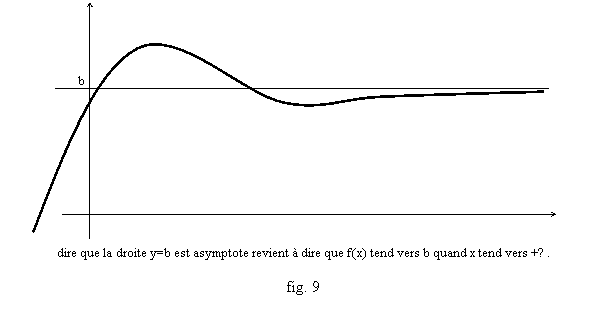
Un dernier cas : branche parabolique verticale.

Reste le cas où f(x)/x a une limite infinie, c’est-à-dire où f(x) tend vers +¥ (ou -¥) plus vite que n’importe quelle droite y=ax. Par analogie avec la fonction x ax², et avec l’allure de courbe que cela suppose, on définit :

Définition : On dit que f a une branche parabolique en direction de l’axe vertical quand x tend vers +¥, si f(x)/x tend vers +¥ ou –¥ quand x tend vers +¥ (fig. 10).

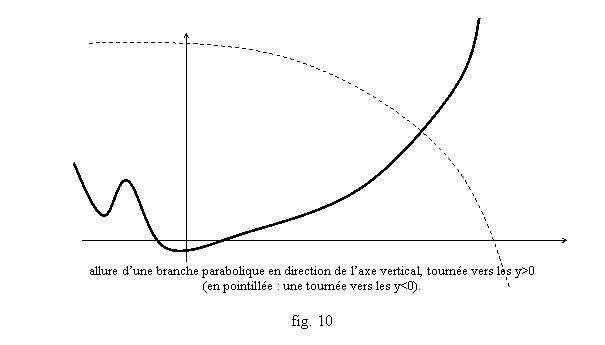
Branche infinie : comment utiliser des développements limités

Ces comportements sont quelques descriptions possibles de l’allure des courbes dans ce qu’on appelle les « branches infinies ». On va donner maintenant une technique de calcul.

Pour les trouver, il y a d’autre moyen que d’étudier le quotient f(x)/x. En fait étudier la fonction f(x) en +¥ et chercher à l’écrire sous la forme ax+b+une fonction (f(x)-ax-b) qui tend vers 0, peut se ramener à un problème connu. Posons g(y)=yf(1/y) pour y>0. Alors en général f(x) tend vers +¥ en +¥ (s’il y a une limite l, c’est que la droite y=l est asymptote), mais f(x)/x a une limite si et seulement si f(1/y)/(1/y)=g(y) a une limite quand y®0⁺.

Supposons connu un d.l. de g en 0 à l’ordre 1 : g(y)=a+by+ye(y). Alors en reprenant x=1/y il vient f(x)/x=g(y)=a+b/x+(1/x)e(1/x) et f(x)=ax+b+e(1/x) où e(1/x) tend vers 0, c’est-à-dire qu’on voit directement que la droite y=ax+b est asymptote.

Cette technique permet de préciser même la position de la courbe par rapport à l’asymptote, ce qu’il faut faire quand ce n’est pas trop dur à calculer – ou quand on nous le demande !

Supposons qu’on ait poussé plus loin le d.l. et qu’il se termine non par ye(y) mais par cy²+y²h(y). Alors en ramenant à f on trouve :

(f(x)/x)=a+b/x+c/x²+h(1/x)/x²

soit en multipliant par x :

f(x)=ax+b+(1/x)(c+h(1/x)).

Comme (1/x) tend vers 0, il y a un intervalle ]A,+¥[ où c+h(1/x) est du signe de c ; donc (1/x)(c+h(1/x)) aussi. Si c>0 le point (x,f(x)) vérifie donc f(x)=ax+b+(1/x)(c+h(1/x))>ax+b et est au dessus du point (x,ax+b) voisin de l’asymptote. Ainsi la droite est au dessus de son asymptote. De même si c<0 elle sera au dessous. On peut donc trouver la position de la droite vis-à-vis de l’asymptote en poussant le d.l. de g jusqu’au terme en y², ou si c=0, jusqu’au premier terme non nul suivant. En –¥ il faut faire attention au signe du 1/x^k en facteur, qui dépend de la parité de k.

Enfin dans certains cas le comportement est moins régulier. Si on prend f(x)=x+sin(x)/x par exemple, f(x)-x=sin(x)/x tend vers 0 en +¥, donc la droite y=x est asymptote, mais le signe de f(x)-x change « tous les  p». On retiendra néanmoins :

Propriété 1 : Si la fonction g(y)=yf(1/y) a un développement limité a+by en 0⁺, alors la droite y=ax+b est asymptote à la courbe de f en +¥. Le terme suivant du d.l. de g donne la position de la courbe par rapport à l’asymptote.

Une fois effectuée l’étude complète d’une fonction, son tableau de variation, ses branches infinies, on peut tracer sa courbe et on doit être en mesure de résoudre facilement des problèmes où cette fonctions intervient : inégalités, équations, etc.

Exemple 1 : Etudier les branches infinies de la fonction f(x)=ln(3^x+1+1).

Comme 3^x+1>0 sur R, on a 3^x+1+1>1>0 et f est définie et continue (composition de fonctions continues) sur R tout entier. Il ne peut donc y avoir de branches infinies que quand x tend vers ±¥.

Quand x tend vers -¥, 3^x tend vers 0 donc 3^x+1+1=3´3^x+1 tend vers 3´0+1=1 et f(x) tend vers ln(1)=0. L’axe des x est donc asymptote horizontale en -¥.

Quand x tend vers +¥, on peut écrire : 3^x+1+1=3^x+1(1+3^-(x+1)). Donc on a :

f(x)=ln[3^x+1(1+3^-(x+1))]=ln(3^x+1)+ln(1+3^-(x+1))=(x+1)ln(3)+ln(1+3^-(x+1)).

Posons e(x)=ln(1+3^-(x+1)). On a toujours 3^-(x+1)>0 donc 1+3^-(x+1)>1 et e(x)=ln(1+3^-(x+1))>0. Par ailleurs si x ® +∞, 3^-(x+1) tend vers 0, donc e(x) tend vers ln(1+0)=0.

Par conséquent la droite y=(x+1)ln(3)=ln(3).x+ln(3) est asymptote à la courbe de f, qui est située au dessus de son asymptote. On peut donc tracer l’allure de cette courbe en l’infini (fig.11) (f est strictement croissante, on le vérifie aisément).

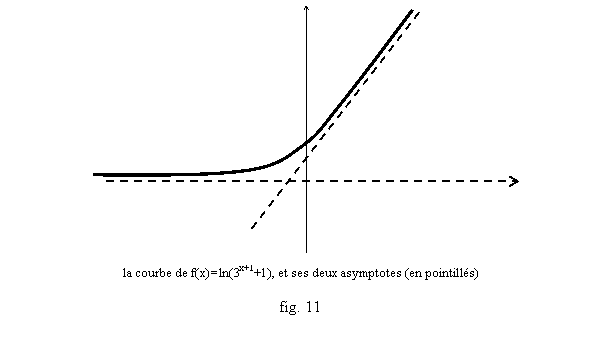
Exemple 2 : Faire l’étude complète de la fonction f(x)=, en précisant les branches infinies.

La fonction est définie quand . L’équation se résout :

donc on a . Sur cet ensemble, comme composition de fonctions continues et dérivables, f est continue et dérivable (la seule fonction intervenant dans f pas forcément dérivable est , pas dérivable en 0. Mais comme c’est qui intervient dans f et que x²+1³1>0, cela n’empêche pas f d’être dérivable partout sur D_f).

Par ailleurs comme f(x) ne dépend que de x² et que (-x)²=x², on a f(-x)=f(x) et f est paire.

On fait donc l’étude de f sur .

En on a des limites infinies. Quel que soit x on a :

Donc le dénominateur est positif et tend vers 0 quand et que x tend vers , tandis que le numérateur tend vers , ce qui fait que f(x) tend vers +∞. Quand tend vers , le numérateur tend toujours vers 3 et le dénominateur vers 0, mais le dénominateur étant négatif, cette fois f(x) tend vers -∞. Donc la courbe a une asymptote verticale, la droite d’équation : . A gauche de la droite, la courbe « plonge », à droite elle « tombe d’en haut ».

Pour trouver les variations de f, calculons la dérivée de f, en utilisant les différentes règles de calcul des dérivées :

(formule de dérivée d’un quotient)

(dérivée d’une composée avec la racine)

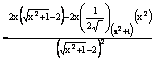(en utilisant les dérivées connues)

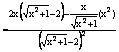(en explicitant toutes les fonctions)

(en mettant au même dénominateur)

(en développant dans la parenthèse)

(car quand a>0)

(en simplifiant les termes)

(en multipliant par la quantité conjuguée)

(grâce à la formule (a-b)(a+b)=a²-b²)

( quand a>0 comme ci-dessus)

Le grand quotient étant positif sur R₊ (et nul en 0), f’(x) est du signe de x⁴-12x²-12. On pourrait étudier son signe en étudiant ses variations (dérivées, etc.). Mais il vaut mieux remarque que c’est t²-12t-12 avec t=x². Calculons =122-4´12=144+48=192=64´3. Il y a donc deux racines en lesquelles t²-12t-12 change de signe, t=[12±8]/2. Seule une de ces deux racines est positives, donc seule elle correspond à des racines (et à chaque fois un changement de signe, puisque x² dépasse la valeur de t correspondante) pour x⁴-12x²-12. Sur R₊ cela donne :

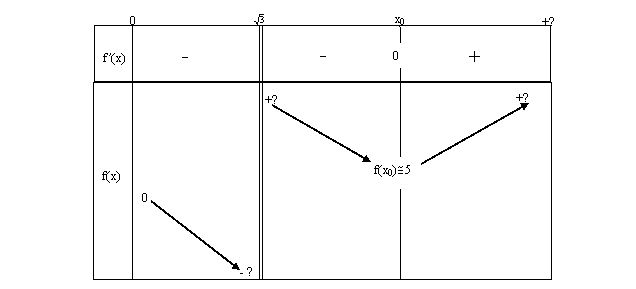
Avant cette valeur, on voit (en essayant par exemple avec x=0) que x⁴-12x²-12<0, et donc f’(x)<0, et après x₀ : f’(x)>0.

Pour préciser les choses, on peut estimer f(x₀) (avec une calculatrice par exemple) :

f(x₀)=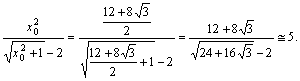

On peut, avec ces données, dresser le tableau de variation.

Reste à faire l’étude en +∞. On peut déjà écrire :

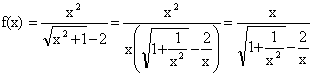
donc, quand x tend vers +∞, 1/x² et 2/x tendant vers 0, le dénominateur tend vers , tandis que le numérateur tend vers +∞, donc f(x) tend vers +∞.

Pour étudier cette branche infinie, posons g(y)=yf(1/y). On a donc :

.

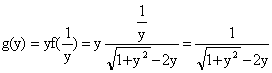On va faire un DL en 0 de cette fonction.

La fonction a pour dérivée , qui vaut 1/2 en 0, donc son d. l. en t=0 à l’ordre 1 est :

, avec .

On peut donc écrire :

avec b(y)=a(y²)®0 quand y ® 0.

On a pour cette fonction un DL₂(0).

Par ailleurs en t=1 on peut écrire :

.

Si on compose les DL obtient en fin de compte :

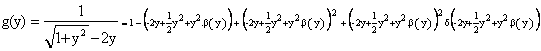
Ce qui donne : f(x)=xg(1/x)=x(1+2/x+(3/2)(1/x²)+(1/x²)e(1/x))=x+2+(1/x)(3/2+h(x)), avec h(x) tendant vers 0 quand x tend vers +∞. Cette écriture prouve que la droite y=x+2 est asymptote à la courbe, et que la courbe est au-dessus de son asymptote puisque la différence f(x)-x-2 est le produit de 1/x>0 par 3/2+h(x) qui tend vers 3/2>0, donc est >0 au moins à partir d’un certain moment.

Voici le tableau de variation de f, et l’allure de son graphe (fig. 12) :

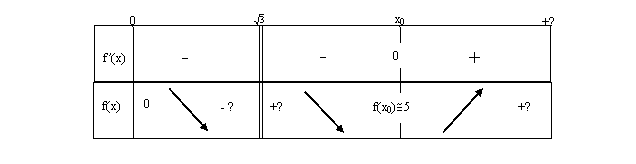
Remarque : on peut, bien sûr, représenter le tableau de variation sur une même ligne :

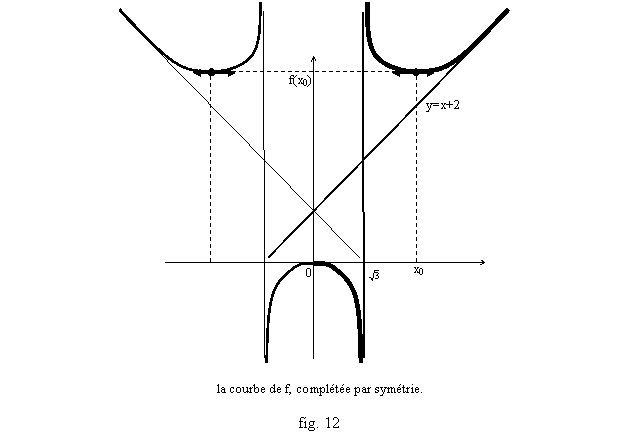
Dans ces deux exemples, on a spécialement détaillé les calculs et les explications. L’habitude doit aider les étudiants à réaliser des calculs – de dérivées notamment, beaucoup plus vite que c’est écrit ici (calcul de la dérivée dans l’exemple 2 par exemple…).

Exercices :

1) Etudier la fonction suivante, en représentant son graphe, et en montrant d’abord qu’on peut prolonger f par continuité sur R tout entier, et que la fonction obtenue reste dérivable : f(x)=sin(x)/x.

2) Mêmes questions avec f(x)=[e^x-1]/x.

3) Mêmes questions avec f(x)=1/sin(x)-1/x.

4) Mêmes questions avec f(x)=ln(x)/[x-1].

5) Etudier les branches infinies des fonctions suivantes : f(x)=E(x) ; f(x)=E(sin(x)) ; f(x)= ; f(x)= ; f(x)=E(x²).

6) Pour les fonctions suivantes, calculer la limite de f(x+1)-f(x), et étudier aussi la branche infinie quand x tend vers +∞ : f(x)=x² ; f(x)=ln(x+1) ; f(x)=e^x ; f(x)=x+. Si on remplace f par la fonction f(x+1)-f(x), montrer qu’au d’un certain nombre de remplacement, on tombe sur 0, si on part de f(x)=xⁿ ; que se passe-t-il si f(x)=e^x ?

7) Etudier les fonctions usuelles suivantes (fonctions « trigonométriques hyperboliques ») : ch(x)=[e^x+e^-x]/2 (cosinus hyperbolique) ; sh(x)=[e^x-e^-x]/2 (sinus hyperboliques) ; th(x)=sh(x)/ch(x). Montrer qu’on a les relations suivantes, pour tous x,y réels :

§ ch²(x)-sh²(x)=1 ;

§ ch(x)+sh(x)=e^x ; ch(x)-sh(x)=e^-x ;

§ ch(x+y)=ch(x)ch(y)+sh(x)sh(y) ;

§ sh(x+y)=ch(x)sh(y)+sh(x)ch(y) ;

§ ch’(x)=sh(x) ; sh’(x)=ch(x) ; th’(x)=1/ch²(x)=1-th²(x).

8) Etudier les fonctions suivantes : f(x)= ; f(x)=.

9) Soit x un réel positif. Montrer qu’il existe une unique solution positive à l’équation en t : t³+xt=1 ; on note f(x) cette solution. Montrer que 0<f(x)<1/x, puis, en admettant que f est dérivable, que f’(x)= -f(x)/[3f²(x)+x]. en déduire les variations et l’allure du graphe de f.

10) Faire une étude semblable pour f(x) solution de l’équation xt³+t=1 ; on montrera que f(x) tend vers +∞ en +∞, et on étudiera les branches infinies de f.

11) Faire l’étude et la représentation complètes des fonctions suivantes :  :  ;  ;  ;  ;  ;  ;  ; .

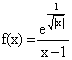12) Soit un paramètre a réel. Etudier la fonction f(x)=(1/x)ln^a(x), en discutant suivant les valeurs de a.