Mathématiques

Cours-TD – Culture Scientifique de base – 2005-2006

Chapitre 3 – Applications de la dérivation, dérivées multiples, développements limités.

1) Dérivées successives et formules de Taylor

On a vu au paragraphe précédent que la dérivée d’une fonction donnait des renseignements sur la fonction elle-même. On va ici pousser cette approche plus loin, et exiger plus de propriétés de la dérivée.

Définition :

§ Soit f une fonction définie sur un intervalle I, dérivable sur I. On dit que f est continûment dérivable, ou de classe C¹, si f’ est continue sur I.

§ Si f’ est dérivable en un point aÎI on dit que f est deux fois dérivable en a et on note f’’(a) le nombre dérivé de f’ au point a. On dit que f est deux fois dérivable sur I si f est deux fois dérivable en tout point de I, et on note alors f’’=(f’)’ la dérivée de f’, appelée fonction dérivée deuxième ou seconde de f.

§ Si f’’ est définie, et dérivable en un point aÎI on dit que f est trois fois dérivable en a et on note f’’’(a) ou f⁽³⁾(a) le nombre dérivé de f’’ au point a. On dit que f est trois fois dérivable sur I si f est deux fois dérivable en tout point de I, et on note alors f⁽³⁾=f’’’=(f’’)’ la dérivée de f’’, appelée fonction dérivée troisième de f.

§ On procède de même, et on définit les dérivées quatrième, cinquième, etc. (on dit aussi dérivées d’ordre 4, d’ordre 5, …). On les note f⁽⁴⁾, f⁽⁵⁾, etc. .

§ Si f est n fois dérivable et que f⁽ⁿ⁾ est continue sur I, on dit que f⁽ⁿ⁾ est n fois continûment dérivable, ou de classe Cⁿ.

§ Enfin si f est n fois dérivable sur I pour tout n, on dit qu’elle est indéfiniment dérivable sur I, ou de classe C^¥ sur I.

Les propriétés donnant les dérivées de fonctions obtenues par opérations, se traduisent pour ces notions de dérivées n-ème :

Propriété 1 : Soient f,g définies sur un intervalle I, et n fois dérivable sur I. Alors :

§ Si k<n, f⁽ⁿ⁾ est aussi la dérivée (n-k)-ème de f^(k).

§ si a,b sont deux réels, la fonction h=a.f+b.g est n fois dérivable sur I, et h⁽ⁿ⁾=a. f⁽ⁿ⁾+b.g⁽ⁿ⁾.

§ f´g est n fois dérivable sur I, et si g ne s’annule pas sur I, f/g est n fois dérivable sur I.

§ Si f :I®J est n fois dérivable et g :J®K est n fois dérivable, gof : I®K est n fois dérivable sur I.

Démonstrations : On va faire les démonstrations pour les rangs 2 et 3. Pour les rangs supérieurs, on reproduit les mêmes raisonnements « de proche en proche ». Bien sûr, dire ceci n’est pas faire une démonstration générale. Au contraire, cela sous-entend qu’il faut refaire une telle preuve dans chaque cas particulier, si on est confronté dans un exercice au cas n=8, par exemple, il faudra recommencer tout, car ce qu’on aura dit pour les cas n=2,3, voire 4,5, ne servira pas. En fait cette façon de prouver les choses « de proche en proche », est valable si on la rédige bien : c’est ce qu’on appelle un raisonnement par récurrence. Mais comme on n’exigera pas des étudiants de savoir les utiliser et les manier à l’issu de ces 6 semaines, on a choisi de ne pas détailler les choses ici.

Pour la première propriété, f⁽²⁾ est bien la dérivée de f’. Et pour n=3, f⁽³⁾ est la dérivée de f⁽²⁾ par définition. Comme f⁽²⁾=(f’)’, f⁽³⁾ est la dérivée de la dérivée de f’, donc la dérivée seconde de f’ par définition de la dérivée seconde : f⁽³⁾=[f’]⁽²⁾.

Regardons la deuxième propriété. h=a.f+b.g est dérivable et h’=(a.f+b.g)’=a.f’+b.g’. On peut alors dériver h’ et on obtient : h(2)=(h’)’=(a.f’+b.g’)’==a.(f’)’+b.(g’)’==a.f⁽²⁾+b.g⁽²⁾.

On peut continuer rang après rang : h⁽³⁾=[h⁽²⁾]’=[a.f⁽²⁾+b.g⁽²⁾]’=a.[f⁽²⁾]’+b.[g⁽²⁾]’=a.f⁽³⁾+b.g⁽³⁾ ; et ainsi de suite…

Pour le produit ou le quotient, les formules de calculs sont plus compliquées, mais on y arrive quand même : si f,g sont deux fois dérivables, comme (fg)’=f’g+fg’ apparaît comme une somme de produit de fonction dérivables (puisque f et g étant deux fois dérivables, f’ et g’ le sont dérivables). Donc chacun des produits f’g et fg’ est dérivable, et leur somme aussi (propriété précédente), ce qui prouve que (fg)’ est dérivable et donc fg deux fois dérivables. Si maintenant f et g sont trois fois dérivables, f’ et g’ sont deux fois dérivables, donc fg’ et f’g sont deux fois dérivable d’après le cas déjà fait, et leur somme (fg)’ est deux fois dérivable, donc fg est trois fois dérivables. On peut continuer : une fois qu’on sait que le produit de deux fonctions trois fois dérivables est trois fois dérivables, si f et g sont quatre fois dérivables, f’ et g’ sont trois fois dérivables, donc f’g et fg’ aussi comme produit, donc leur somme (fg)’ est trois fois dérivable et (fg) est 4 fois dérivables, etc. . Pour le quotient, c’est pareil, à partir de la formule pour le rang 1 : (f/g)’=(f’g-g’f)/g2.

Pour la composition, comme on a (gof)’=f’(g’of) est le produit d’une composée g’of et de f’, des fonctions dérivables un cran de moins que f et g, on peut appliquer le même principe. Ainsi, si f et g sont deux fois dérivables, f’, g’, f sont chacune au moins une fois dérivable, donc g’of aussi et f’(g’of)=(gof)’ est dérivable, et gof est deux fois dérivable. Comme conséquence, si f et g sont trois fois dérivables, f’ et g’ le sont deux fois et donc g’of aussi, donc le produit (gof)’=f’(g’of) est deux fois dérivable, et gof est trois fois dérivable, etc. .

Tous ces résultats sont aussi vrais ponctuellement (pour calculer la dérivée n-ème en un point).

Exemples : fonctions usuelles.

§ Posons f(x)=C constante. Comme f’=0, les dérivées d’ordres supérieurs sont définies mais toutes nulles ;

§ Posons f(x)=ax+b affine. f’(x)=a, comme on l’a vu. Comme la dérivée f’ est une constante, les dérivées d’ordres supérieurs sont toutes nulles : f⁽²⁾=f⁽³⁾=…=0.

§ Si f(x)=x², f’(x)=2x, donc on est dans le cas précédent pour les dérivées suivantes, et f’’(x)=2, f⁽³⁾=f⁽⁴⁾=…=0.

§ Plus généralement, les dérivées successives de x³ sont 3x², 3(2x)=6x, 6, 0, 0, … ; celles de x⁴ sont 4x³, 4(3x²)=12x², 12(2x)=24x, 24, 0,0,0, … ; on voit mieux les choses en effectuant pas les produits : les dérivées de x4 sont par exemple 4x³, (4´3)x², (4´3´2)x, (4´3´2´1), 0,0,0, … ; celles de x⁵ : 5x⁴, (5´4)x³, (5´4´3)x², (5´4´3´2)x, (5´4´3´2´1), 0,0, … .

§ On peut généraliser : si on dérive n fois la fonction x a x^k, on obtiendra 0 si k<n, et sinon un coefficient k(k-1)(k-2)…(k-(n-1)) fois la fonction x^k-n. On écrit souvent ce coefficient avec des factorielles : , et on en tire :

Si k<n, [x^k]⁽ⁿ⁾=0, si k=n, [x^k]^(k)=k !, si k>n, [x^k]⁽ⁿ⁾=[k !/(k-n) !]x^k-n.

§ Un polynôme, une fraction rationnelle sur un intervalle où elle est définie, est indéfiniment dérivable. Si P(x)=a₀+a₁x+…+a_kx^k on a, comme on le voit grâce aux calculs précédents, P⁽ⁿ⁾(x)=n !a_n+(n+1) !a_n+1x+[(n+2) ! /2 !]a_n+2x²+…+[k !/(n-k) !]a_kx^k-n. Une fraction rationnelle, comme quotient de fonctions indéfiniment dérivables, et dérivable.

§ A étant un réel quelconque, la fonction x a x^a est dérivable sur R₊^*, de dérivée ax^a-1. Elle est donc deux fois dérivable, de dérivée seconde égale à a[x^a-1]’=a(a-1)x^a-2, et trois fois dérivable de dérivée troisième égale à a(a-1)(a-2)x^a-3, etc. . On peut généraliser :

La dérivée n-ème de x a x^a existe et vaut a(a-1)(a-2)…(a-(n-1))x^a-n.

^§ En particulier, 1/x est indéfiniment dérivable, et comme c’est la dérivée de ln, ln est indéfiniment dérivable. On peut calculer cette dérivée, grâce à la formule précédente : (1/x)⁽ⁿ⁾=(x^-1)⁽ⁿ⁾

=(-1)(-1-1)(-1-2)…(-1-(n-1))x^-1-n

=(-1)(-2)…(-n)x^-(n+1)

=(-1)…(-1)(12…n)/xⁿ⁺¹

=(-1)ⁿn !/xⁿ⁺¹

et donc : ln⁽ⁿ⁾(x)=(1/x)^(n-1)=(-1)^n-1(n-1) !/xⁿ.

§ Comme exp’(x)=exp(x), il s’ensuit que exp est indéfiniment dérivable de dérivée n-ème égale à elle-même sur R.

§ De même par composition, x aa^x et x aLog_a(x) ; leur dérivées n-èmes sont données par les formules : lnⁿ(a)a^x et (-1)^n-1(n-1) !/[ln(a)xⁿ]. En effet les dérivées premières sont [a^x]’=[e^xln(a)]’=ln(a)e^xln(a)=ln(a)a^x, et [Log_a(x)]’=[ln(x)/ln(a)]’=(1/x)(1/ln(a)).

§ Comme sin’(x)=cos(x) et cos’(x)= -sin(x), les fonctions sin, cos sont indéfiniment dérivables, et les dérivées successives de sinus sont : cos, -sin, -cos, sin, cos, -sin, -cos, etc., tandis que celles de cosinus sont : -sin, -cos, sin, cos, -sin, -cos, sin, cos, etc. . On peut résumer ceci :

sin^(2k)(x)=(-1)^ksin(x) ; sin^(2k+1)(x)=(-1)^kcos(x).

cos^(2k)(x)=(-1)^kcos(x) ; cos^(2k+1)(x)=(-1)^k+1sin(x).

§ La fonction tangente est indéfiniment dérivable là où elle est définie, comme quotient de fonctions indéfiniment dérivables.

On utilisera à l’occasion des dérivées successives pour les études de fonctions. Par exemple si le signe de la dérivée n’est pas facile à déterminer, on peut étudier la dérivée seconde, en déduire le tableau de variation de la dérivée pour avoir son signe, et en conclure sur la fonction.

L’intérêt essentiel des dérivées n-èmes ici, sera de permettre de calculer une approximation de la fonction f, sur des intervalles ou au voisinage d’un point, raffinant ce qu’on a déjà pour la dérivée, qui fournit une approximation ponctuelle de f, puisque f(x)»f(a)+(x-a)f’(a), avec une erreur qui s’amenuise devant (x-a) quand x tend vers a : on a pris pour cela (cf. chapitre 2) la fonction affine qui vaut autant que f en a, et dont la dérivée (c’est-à-dire la pente) a la même valeur f’(a) que celle de f en a.

On va chercher un polynôme de degré n, construit à partir des dérivées k-èmes en a, qui approcherait f convenablement au voisinage de a. La suite logique de cette démarche est de prendre le polynôme qui présente les mêmes valeurs des n premières dérivées en a.

Propriété-définition : Soit f une fonction définie sur un intervalle I, et n fois dérivable au point a. Alors l’unique polynôme P de degré n tel que P(a)=f(a), P’(a)=f’(a), …, P⁽ⁿ⁾(a)=f⁽ⁿ⁾(a) est le polynôme suivant, appelé polynôme de Taylor de degré n de f au point a (bien qu’on puisse juste dire qu’il est de degré £n) :

.

Démonstration : Soit Q un polynôme de degré n et exprimons Q en fonction de x-a. C’est encore un polynôme de degré n, obtenu en écrivant Q(x) sous la forme Q((x-a)+a)=Q(t+a) avec t=x-a, et en développant les (t+a)^k de Q(t+a) (par exemple (t+a)²=t²+2at+a², (t+a)³=t³+3at²+3a²t+a³, etc., on peut trouver un tel développement pour toute puissance, ce qui montre que le terme de plus haut degré est bien en tⁿ). Si on écrit R(t)=a₀+a₁t+a₂t²+…+a_ntⁿ, on a donc Q(x)=Q(x-a+a)=R(x-a), c’est-à-dire Q(x)=a₀+a₁(x-a)+…+a_k(x-a)^k+…+a_n(x-a)ⁿ. Maintenant les formules précédemment données montrent que Q^(k)(x)=k!a_k+(k+1)!a_k+1(x-a)+(k+2)!a_k+2(x-a)²/2+…+n!a_n(x-a)^n-k/(n-k)!, d’où Q^(k)(a)=k!a_k. Ainsi les nombres Q^(k)(a) sont égaux aux nombres f^(k)(a) si et seulement si on a pour chaque k : a_k=Q^(k)(a)/k!= f^(k)(a)/k!.

On va voir que le polynôme de Taylor de degré n permet d’approcher la fonction mieux que toute autre polynôme de même degré. De même que la fonction affine « tangente », qui colle à la courbe alors que les autres fonctions affines présentent un angle avec elle (cf. chapitre 2), de même le polynôme de Taylor de degré 2 sera la parabole qui colle « le mieux possible » à la courbe (fig. 1), et ainsi de suite… .

On va chercher une propriété de limite, du type f(x)-P(x) est « très » petit quand x tend vers a, si P est le polynôme de Taylor de degré n au point a. En fait on sait déjà que c’est vrai pour n=1, et on a vu que suffisamment petit voulait dire infiniment petit devant (x-a). Au degré n, on va chercher une notion semblable. On commence, pour rendre la rédaction plus facile, par étudier le cas où P est le polynôme nul. Le résultat se formulera de la manière suivante : si P=0, c’est-à-dire si tous les coefficients

Propriété 4 : Soit f une fonction. On suppose que sur un intervalle autour de a, ]a-r,a+r[, avec r>0, f est n-1 fois dérivable avec f^(k)(a)=0 si 1£k<n, et f(a)=0. On suppose en outre que f est n fois dérivable au point a et f⁽ⁿ⁾(a)=0. Alors f(x)/(x-a)ⁿ tend vers 0 si x tend vers a (fig. 2).

Démonstration : On fait les premiers cas. Et comme les démonstrations utilisent la vraie définition de la limite, ce n’est pas grave si, à ce niveau, les lecteurs l’occultent. On la donnera en petits caractères.

Supposons donc f(a)=0, f dérivable en a avec f’(a)=0.

La dérivée étant la limite de [f(x)-f(a)]/(x-a) quand x tend vers a, on a :

f(x)/(x-a)=[f(x)-f(a)]/(x-a) ® 0=f’(a).

Supposons maintenant f(a)=f’(a)=f’’(a)=0. Alors d’après ce qui précède appliqué à f’, quand x tend vers a, le quotient [f’(x)-f’(a)]/(x-a)=f’(x)/(x-a) tend vers 0. D’après la définition de la limite donnée au chapitre 1 cela signifie : pour tout nombre e>0, on peut trouver un petit intervalle I_e autour de a sur lequel

f’(x)/(x-a)Î]-e,e[

ou encore :

|f’(x)/(x-a)|<e.

Ceci s’écrit aussi |f’(x)|<e|x-a|. Sur la partie de I_e qui est à droite de a, on a donc :

-e(x-a)<f’(x)<e(x-a).

Ces trois fonctions sont les dérivées de - e(x-a)²/2, f(x), e(x-a)²/2. D’après l’inégalité des accroissements finis, cela implique que, pour tout x dans cet intervalle, on aura :

- e(x-a)²/2-[-e(a-a)²/2]<f(x)-f(a)<e(x-a)²/2-e(a-a)²/2, donc

- e(x-a)²/2<f(x)<e(x-a)²/2, et :

- e/2<<e/2

Ceci est vrai sur toute la partie droite de I_e. Sur la partie gauche, on obtient la même inégalité mais dans le calcul il faut prendre garde : c’est e(x-a) qui est négatif, et -e(x-a) qui est positif.

Ainsi on trouve des intervalles, toujours plus petits, où le quotient est aussi petit que l’on veut, c’est la « vraie » définition de la limite : .

On peut esquisser comment passer de l’ordre 2 à l’ordre 3 : Si f(a)=f’(a)=f’’(a)=f’’’(a)=0, alors en appliquant le calcul précédent à l’ordre 2 à la fonction f’, on peut affirmer que f’(x)/(x-a)² tend vers 0 quand x tend vers a. Cela entraîne qu’on peut obtenir des encadrements du type -e<f’(x)/(x-a)²<e, ou encore

-e(x-a)²<f’(x)< e(x-a)²,

en prenant x sur un intervalle assez proche de a. Ce sont les dérivées des fonctions

-e(x-a)³/3, f(x), e(x-a)³/3,

et on en tire que c’est le quotient f(x)/(x-a)³ qu’on a réussi à rendre tout petit. On aura bien :

.

On peut ainsi, de proche en proche, généraliser cette propriété.

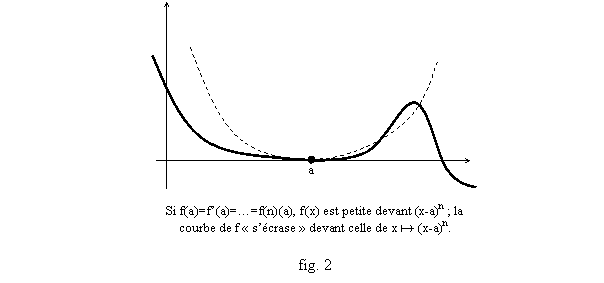
Théorème 5 (formule de Taylor-Young) : Soit f une fonction définie au voisinage d’un point a, et n-1 fois dérivable dans un intervalle ]a-r,a+r[. On suppose que f est n fois dérivable au point a et que P est le polynôme de Taylor de degré n de f en a. Alors on a :

[(f(x)-P(x))/(x-a)ⁿ] ® 0 si x ® a, c’est-à-dire :

[f(x)-f(a)-(x-a)f’(a)-…-(x-a)ⁿ f⁽ⁿ⁾(a)(x-a)ⁿ/n!]/(x-a)ⁿ ® 0 si x ® a.

Démonstration : on applique la propriété 4 à f(x)-P(x), qui a toutes ses dérivées nulles jusqu’à l’ordre n puisque [f-P]^(k)(a)=f^(k)(a)-P^(k)(a) et que P est choisi exprès pour avoir f^(k)(a)=P^(k)(a) pour k=0,1,…,n.

Cette formule est la clef pour de nombreux calculs de limites. On va rendre ceci systématique au prochain paragraphe.

Exercices :

1) Calculer la dérivée seconde des fonctions suivantes : tan(x) ; x^x ;sin(cos(x)).

2) Quelles sont les fonctions deux fois dérivables dont la dérivée seconde est nulle ? Et celle dont la dérivée troisième est nulle ? Généraliser.

3) f est une fonction dérivable sur R, deux fois dérivable en a, telle que f’(a)=0. Montrer que, si f’’(a)>0, f présente un minimum local strict en a. Si f’’(a)<0, que se passe-t-il ?

4) On pose f(x)=ln(1+x).

a. Calculer la dérivée n-ème en 0 de la fonction f.

b. Soit x tel que -1<x<1, et n un entier ; démontrer la relation :

1-x+x²-…+(-1)ⁿxⁿ=.

c. Montrer qu’on a pour tout xÎ]0,1[ et tout n entier, |-[1-x+x²-…+(-1)ⁿxⁿ]|£xⁿ⁺¹.

d. En déduire que pour tout xÎ]0,1[ et tout entier n, on a l’inégalité :

|ln(x+1)-[x-x²/2+x³/3-…+(-1)ⁿxⁿ⁺¹/(n+1)]|£xⁿ⁺²/(n+2).

e. Que se passe-t-il quand xÎ]-1,0[ ?

2) Montrer qu’on a les inégalités, vraies pour tout x :

|cos(x)-1+x²/2|£|x|⁴/24, |sin(x)-x|£|x|³/6.

3) Soit f(x)=0 si x£0, f(x)=e^-1/x si x>0.

a. Montrer par récurrence sur n qu’il existe un polynôme P_n tel que pour tout x>0, f⁽ⁿ⁾⁽x)=[P_n(x)/x²ⁿ]e^-1/x.

b. Montrer que f est indéfiniment dérivable, avec f⁽ⁿ⁾(0)=0.

c. Ecrire la formule de Taylor à l’ordre n entre 0 et x de f.

Que pensez-vous de l’énoncé suivant : « Soient F et G deux fonctions indéfiniment dérivables dans un intervalle I, a un point de I tel que, pour tout n, F et G ait le même polynôme de Taylor d’ordre n en a, alors il y a un intervalle ]a-r,a+r[, avec r>0, sur lequel F(x)=G(x). »

6) Soit f une fonction (n-1) fois dérivable telle que l’équation f(x)=0 a n solutions distinctes dans un intervalle I. Montrer que pour k<n, l’équation f^(k)(x)=0 a au moins (n-k) racines distinctes dans I.

2) Développements limités

On va chercher à formaliser les approximations locales d’une fonction f, au voisinage d’un point x₀ ; pour une dérivée, on a vu que cela correspondait à lever l’indétermination 0/0 de (f(x)-f(a))/(x-a) au voisinage de a, et cela revenait à écrire f(x) sous la forme A+B(x-a)+g(x) où g est une fonction « négligeable devant toute fonction affine » quand x tend vers a, c’est-à-dire de la forme (x-a)e(x) avec e(x) tendant vers 0 si x tend vers a. On va systématiser cette approche. L’approximation de fonctions par des polynômes semble facilement généralisable quand on voit la formule de Taylor-Young (chapitre 4, paragraphe 3) :

Définitions :

1- Soit f une fonction définie sur un voisinage (ou voisinage à gauche, à droite, strict) d’un réel x₀. On appelle développement limité à l’ordre n de f au voisinage de x₀ tout polynôme P de degré inférieur ou égal à n tel que f s’écrive f(x)=P(x)+(x-x₀)ⁿe(x), pour une fonction e telle que e(x) tende vers 0 quand x tend vers x₀.

2- Ecriture : si P(x) est un développement limité de f en x0 à l’ordre n, on exprimera cette propriété (longue à écrire !) en disant que P(x) est un (en fait le) « DL d’ordre n en x₀ de f », ou plus simplement « le DL_n(x₀) de f ».

3- Si une fonction a(x) s’écrit (x-x₀)ⁿe(x), où e(x) est une fonction qui tend vers 0 quand x tend vers x₀, on dira que a(x) est négligeable devant (x-x₀)ⁿ quand x tend vers x₀ (ou simplement : « négligeable devant (x-x₀)ⁿ en x₀ »). Cela revient à dire que le polynôme constant égal à 0 est DL de a(x) à l’ordre n en x₀.

Propriété 1 :

i) La fonction a(x) est négligeable devant (x-x₀)ⁿ en x₀, si et seulement si : .

ii) Si m<n, (x-x₀)ⁿ est négligeable devant (x-x₀)^m en x₀, et pour toute fonction a :

a(x) négligeable devant (x-x₀)ⁿ en x₀Þ a(x) négligeable devant (x-x₀)^m en x₀.

iii) Si f admet P pour DL. d’ordre n en x₀ et si f-g est négligeable devant (x-x₀)ⁿ en x₀, alors g admet P pour DL d’ordre n en x₀.

iv) Dire que la fonction a est négligeable à l’ordre 0 en x₀ signifie juste « a(x) tend vers 0 quand x tend vers x₀ » et écrire un développement limité d’ordre 0 d’une fonction f, c’est juste une écriture de la forme f(x)=l+e(x), avec e(x) tendant vers 0 en x₀, c’est-à-dire que cela revient à dire que f a une limite en x₀.

v) Dire que la fonction a est négligeable à l’ordre 1 en x₀ signifie juste que la fonction a, valant 0 en x₀, a une dérivée nulle en x₀, et dire que la fonction f a P(x)=ux+v comme DL d’ordre 1 en x₀ revient à dire que f est dérivable en x₀ de dérivée u (et alors v=f(x₀)-ux₀). Ce DL s’écrit en général sous la forme :

P(x)=f(x₀)+f’(x₀)(x-x₀)

(le terme « d’ordre 0 » f(x₀), valeur limite de f, et le terme « d’ordre 1 » f’(x₀)(x-x₀), proportionnel à la différence x-x₀, sont ainsi bien en évidence)

vi) Plus généralement si f est n fois dérivable en x₀, le polynôme

P(x)=f(x₀)+f '(x₀)(x-x₀)+…+(f⁽ⁿ⁾(x₀)/n!)(x-x₀)ⁿ

est un DL de f en x₀ à l’ordre n.

Démonstration :

i) Dire que a(x) s’écrit (x-x₀)ⁿe(x), où e(x) est une fonction qui tend vers 0 quand x tend vers x₀, revient à dire que si on pose , on obtient une fonction qui tend vers 0. Les deux formulations sont bien équivalentes.

ii) L’égalité suivante est évidente : (x-x₀)ⁿ=(x-x₀)^n-m(x-x₀)^m. Si on pose e(x)=(x-x₀)^n-m, e(x) tend vers 0 quand x tend vers x₀ car l’exposant n-m est au moins égal à 1, et donc :

(x-x₀)ⁿ=e(x)(x-x₀)^m est bien négligeable devant (x-x₀)^m en x₀.

Si a(x) est négligeable devant (x-x₀)^m en x₀, c’est-à-dire s’écrit h(x)(x-x₀)ⁿ où h(x) tend vers 0, alors a(x) s’écrit aussi d(x)(x-x₀)^m en posant d(x)=h(x)(x-x₀)^n-m, donc est négligeable devant (x-x₀)^m.

iii) Les hypothèses sont : 1) f(x)=P(x)+(x-x₀)ⁿe₁(x) ; 2) f(x)-g(x)=(x-x₀)ⁿe₂(x) ; avec des fonctions e₁ et e₂ qui tendent vers 0 quand x tend vers x₀. Alors on a :

g(x)=[g(x)-f(x)]+f(x)= -(x-x₀)ⁿe₂(x)+P(x)+(x-x₀)ⁿe₁(x)=P(x) +(x-x₀)ⁿ[e₁(x)- e₂(x)].

Or e₁-e₂ qui tend vers 0-0=0 quand x tend vers x₀, donc P est un DL_n(x₀) de g.

iv) Une fonction négligeable à l’ordre 0 en x₀ est une fonction qui s’écrit e(x)(x-x₀)⁰ (car on a (x-x₀)⁰=1), avec e(x) tendant vers 0 en x₀. Un polynôme de degré inférieur ou égal à 0 étant une constante C, écrire un DL d’ordre 0 revient à écrire f(x)=C+e(x) avec e(x) tendant vers 0, ce qui est équivalent à : « f(x) a pour limite C en x₀ ».

v) Les DL à l’ordre 1 sont des écritures vues dans le chapitre sur la dérivation.

vi) Ecrivons la formule de Taylor à l’ordre n de f en x₀. On a vu :

[f(x)-f(x₀)+f '(x₀)(x-x₀)+…+(f⁽ⁿ⁾(x₀)/n!)(x-x₀)ⁿ]/(x-x₀)ⁿ ® 0 quand x ® x₀.

Posons P(x)=f(x₀)+f '(x₀)(x-x₀)+…+(f⁽ⁿ⁾(x₀)/n!)(x-x₀)ⁿ et :

e(x)=[f(x)-f(x₀)+f '(x₀)(x-x₀)+…+(f⁽ⁿ⁾(x₀)/n!)(x-x₀)ⁿ]/(x-x₀)ⁿ=[f(x)-P(x)]/(x-x₀)ⁿ.

On vient de voir que, d’après la formule de Taylor, e(x) ® 0 quand x ® x₀. Or écrire :

e(x)=[f(x)-P(x)]/(x-x₀)ⁿ.

Revient à écrire :

e(x)(x-x₀)ⁿ=f(x)-P(x)

ou encore f(x)=P(x)+e(x)(x-x₀)ⁿ, ce qui prouve que P est un développement limité de f à l’ordre n en x₀.

L’intérêt des développements limités est qu’on peut calculer avec, sans passer à chaque fois par la formule de Taylor. Mais :

ATTENTION ! Les raisonnements qu’on est amené à faire, pour rester dans un cas général, se traduisent par des calculs horriblement compliqués, avec beaucoup de notations. Déjà un polynôme de degré n suppose n+1 coefficients, qu’on note avec des indices : a₀, a₁, …, a_n, et quand il y a plusieurs polynômes, c’est pire. Alors les étudiants noyés par ces débauches de lettres et de formules peuvent se contenter de lire les règles de calcul, et de regarder l’illustration par des exemples qu’on donnera à la suite (souvent la démonstration consiste à faire le même calcul que dans les exemples, mais avec des lettres au lieu des nombres particuliers).

Propriété 2 : Soient f,g deux fonctions admettant les polynômes P et Q comme DL d’ordre n en x₀, et soient a,b deux réels. Alors on obtient un DL à l’ordre n en x₀ de la fonction (a.f+b.g) en calculant le polynôme x a a.P(x)+b.Q(x).

Démonstration :

Les hypothèses sont : on peut trouver deux fonctions e₁ et e₂ tendant vers 0 en x₀ telles que, pour tout x :

f(x)=P(x)+(x-x₀)ⁿe₁(x) et g(x)=Q(x)+(x-x₀)ⁿe₂(x).

Alors on aura aussi, pour tout x :

(*) (af+bg)(x)=a[P(x)+(x-x₀)ⁿe₁(x)]+b[Q(x)+(x-x₀)ⁿe₂(x)]=(aP+bQ)(x)+(x-x₀)ⁿ(ae₁+be₂)(x)

Or la fonction a.e₁+b.e₂ tend vers a´0+b´0=0 en x₀.

Il reste à remarquer que si P(x)=a₀+a₁x+…+a_nxⁿ, et Q(x)=b₀+b₁x+…+b_nxⁿ, sont les écritures de P et Q comme polynômes de degrès inférieurs ou égaux à n, alors :

(aP+bQ)(x)=a(a₀+a₁x+…+a_nxⁿ)+b(b₀+ …+b_nxⁿ)=(aa₀+bb₀)+(aa₁+bb₁)x+…+(aa_n+bb_n)xⁿ

est aussi un polynôme de degré inférieur ou égal à n. Cette remarque et l’égalité (*) prouvent que aP+bQ est bien le DL_n(x₀) de af+bg.

Exemple : calculer un DL de sin(x)+cos(x) en p/6 à l’ordre 2.

On utilise la formule de Taylor, valable puisque les fonctions sont deux fois dérivables. Comme sin(p/6)=1/2, cos(p/6)=/2, on a aussi :

sin’(p/6)=cos(p/6)=/2, sin’’(p/6)=-sin(p/6)= -1/2

cos’(p/6)= -sin(p/6)=-1/2, cos’’(p/6)= -cos(p/6)= -/2.

Donc on aura :

sin(x)=sin(p/6)+(x-p/6)sin’(p/6)+(1/2)(x-p/6)²sin’’(p/6)+(x-p/6)²e₁(x)

=1/2+(/2)(x-p/6)-(1/4)(x-p/6)²+(x-p/6)²e₁(x), avec .

et de même :

cos(x)=/2-(1/2)(x-p/6)-(/4)(x-p/6)²+(x-p/6)²e₂(x) , avec .

On peut donc additionner :

sin(x)+cos(x)=1/2+(/2)(x-p/6)-(1/4)(x-p/6)²+(x-p/6)²e₁(x)

+[/2-(1/2)(x-p/6)-(/4)(x-p/6)²+(x-p/6)²e₂(x)]

=[1/2+(/2)]+[(/2)-(1/2)](x-p/6)+[-(1/4)-(/4)](x-p/6)²

+(x-p/6)²e₁(x)+(x-p/6)²e₂(x)

=(1/2+3/2)+(/2-/2)(x-p/6)+[-1/4-3/4](x-p/6)²+(x-p/6)²[e₁(x)+e₂(x)]

=2-(x-p/6)²+(x-p/6)²e(x)

en posant e(x)=e₁(x)+e₂(x), qui tend vers 0+0=0 quand x tend vers p/6.

On a donc bien obtenu le d. l. de la fonction étudiée :

sin(x)+cos(x)=2-(x-p/6)²+(x-p/6)²e(x)

Remarque : on fait bien attention à garder l’écriture des termes en (x-p/6) sans développer, d’abord parce que ce sont ces termes qui sont significatifs, chacun étant de plus en plus petit devant le précédent, et ensuite parce que, en développant, on trouverait des formules inextricables.

Pour le produit, on peut aussi multiplier les égalités exprimant les DL. Mais le problème est que le produit de deux polynômes de degré n et m est de degré n+m : il faut donc savoir quoi faire des termes de degrés supérieurs à ceux qui sont utiles. La réponse est simple : il faut les ignorer. Pour cela on a besoin de quelques résultats sur les polynômes.

Propriété 3 : Soit P un polynôme, n un entier et x₀ un réel. Alors il y a un unique polynôme R de degré inférieur ou égal à n tel que P(x)-R(x) est négligeable devant (x-x₀)ⁿ en x₀. On l’obtient en écrivant P en fonction de x-x₀ : P(x)=a₀+a₁(x-x₀)+…+a_p(x-x₀)^p où p est le degré de P, et en enlevant tous les termes de degré >n, soit R(x)=a₀+a₁(x-x₀)+…+a_n(x-x₀)ⁿ si n<p, R=P sinon.

Définition : Le polynôme R, associé à P, n et x₀ par la propriété 3, s’appelle troncature de P à l’ordre n en x₀, et se notera (dans le poly uniquement) P_x0,n.

Démonstration de la propriété 3 : On sait que si P est un polynôme de degré p et x₀ est un réel on peut écrire P sous la forme proposée. Pour le vérifier il suffit d’écrire P sous sa forme habituelle :

P(x)=c₀+c₁x+…+c_px^p avec c_p¹0,

et d’exprimer la fonction de la variable u : P(x₀+u)=c₀+c₁(x₀+u)+…+c_p(x₀+u)^p, comme un polynôme écrit sous forme habituelle en u. En effet, en développant les termes (x₀+u)^k, on obtiendra des termes en x₀^ju^k-j, et finalement le tout donnera un polynôme en u, de degré p puisque le seul terme en u^p viendra de c_p(x₀+u)^p=c_p(u^p+… ). Ainsi P(x₀+u) est un polynôme de degré p en u, donc P(x)=P(x₀+(x-x₀)) est bien un polynôme de degré p en x-x₀. On peut donc l’écrire sous la forme :

P(x)=a₀+a₁(x-x₀)+…+a_p(x-x₀)^p.

Considérons un autre polynôme écrit de la même manière :

S(x)=b₀+b₁(x-x₀)+…+b_q(x-x₀)^q.

On va montrer que, si P(x)-S(x) est négligeable devant (x-x₀)ⁿ en x₀, alors les coefficients de P (a₀, a₁, …) et S (b₀,b₁, …) sont les mêmes jusqu’à l’ordre n.

On raisonne par l’absurde : on suppose qu’il y a k£n tel que a_k¹b_k. On peut supposer qu’on a pris le premier k de la sorte. Donc a₀=b₀, a₁=b₁, …, a_k-1=b_k-1 et a_k¹b_k. Alors :

P(x)-S(x)=(a_k-b_k)(x-x₀)^k+(a_k+1-b_k+1)(x-x₀)^k+1+… .

Or on a supposé que cette fonction est négligeable devant (x-x₀)ⁿ en x₀ à S, c’est-à-dire que (P(x)-S(x))/(x-x₀)ⁿ tend vers 0 quand x tend vers x₀ (cf. Propriété 1, point i)). Alors le quotient :

(P(x)-S(x))/(x-x₀)^k=[(P(x)-S(x))/(x-x₀)ⁿ](x-x₀)^n-k

tend vers 0.0^n-k=0 car k£n. Mais cette fonction s’écrit (a_k-b_k)+(a_k+1-b_k+1).(x-x₀)+… qui tend donc vers a_k-b_k+(a_k+1-b_k+1).0+…=a_k-b_k quand x tend vers x₀. On doit donc avoir a_k-b_k=0, ce qui contredit l’hypothèse faite : celle-ci était par conséquent absurde, il est impossible de trouver un k tel que a_k¹b_k.

On a donc forcément a₀=b₀, a₁=b₁ ,… jusqu’à a_n=b_n (=0 si ces degrés ne sont pas atteints dans P ou S). Cela montre que seul le polynôme R décrit dans l’énoncé peut, parmi les polynômes de degré inférieur ou égal à n, vérifier que P(x)-R(x) est négligeable devant (x-x₀)ⁿ en x₀ à P. Réciproquement ce polynôme R vérifie :

- si p>n, P(x)=R(x)+a_n+1(x-x₀)ⁿ⁺¹+…+a_p(x-x₀)^p=R(x)+(x-x₀)ⁿe(x) avec :

e(x)=a_n+1(x-x₀)+a_n+2(x-x₀)²+…+a_p(x-x₀)^n-p

qui tend vers a_n+1.0+a_n+2.0²+…+a_p.0^n-p=0 quand x tend vers x₀  donc P est tangente à l’ordre n en x₀ à R ;

- sinon, P=R donc P(x)-R(x) est négligeable devant (x-x₀)ⁿ, car elle est nulle.

Exemple : tronquer le polynôme P(x)=1+2x+3x²+4x³ à l’ordre 2 en x=1. On peut pour cela utiliser la propriété que (x-1) se factorise toujours dans P(x)-P(1). Donc on aura :

P(x)=P(x)-P(1)+P(1)

=(1+2x+3x²+4x³-(1+2´1+3´1²+4´1³))+P(1)

=(1-1)+2(x-1)+3(x²-1²)+4(x³-1³)+(1+2´1+3´1²+4´1³)

=2(x-1)+3(x-1)(x+1)+4(x-1)(x²+x´1+1²)+10

=(x-1)[2+3(x+1)+4(x²+x+1)]+10

=(x-1)[2+3+4+(3+4)x+4x²]+10

=(x-1)[9+7x+4x²]+10

On peut recommencer la même factorisation pour le polynôme 4x²+7x+9 :

9+7x+4x²=9+7x+4x²-(9+7´1+4´1²)+(9+7´1+4´1²)

=(9-9)+7(x-1)+4(x²-1²)+(9+7+4)

=7(x-1)+4(x-1)(x+1)+20

=(x-1)(7+4(x+1))+20

=(x-1)(11+4x)+20

Et enfin 11+4x=11+4x-11-4´1+(11+4´1)=4(x-1)+15.

Finalement on a :

P(x)=(x-1)[9+7x+4x²]+10

=(x-1)[(x-1)(11+4x)+20]+10

=(x-1)²(11+4x)+20(x-1)+10

=(x-1)²(4(x-1)+15)+20(x-1)+10

=4(x-1)³+15(x-1)²+20(x-1)+10

On a donc l’expression de P en fonction de x-1, et la troncature s’écrit :

P_1,2(x)=10+20(x-1)+15(x-1)².

De cette propriété on tire tout de suite plusieurs propriétés fondamentales des DL.

Propriété 4 : Si f est une fonction définie au voisinage de x₀, alors si f admet un développement limité P à l’ordre n en x₀, P est unique (et ses coefficients le sont). En particulier si f est n fois dérivable en x₀ et si P(x)=a₀+a₁(x-x₀)+…+a_n(x-x₀)ⁿ, alors les seuls coefficients possibles sont : a₀=f(x₀), a₁=f’(x₀),…, a_n=f⁽ⁿ⁾(x₀)/n !. Si P est ce développement, alors les troncatures de P aux ordres m£n constituent les développements limités de f aux ordres m correspondants.

Démonstration : si P, Q sont deux DL de f à l’ordre n, qui s’écrivent

P(x)=a₀+a₁(x-x₀)+…+a_n(x-x₀)ⁿ et Q(x)=b₀+b₁(x-x₀)+…+b_n(x-x₀)ⁿ,

alors d’après la propriété d’addition des DL, le polynôme P(x)-Q(x) est un DL à l’ordre n en x₀ de la fonction f(x)-f(x)=0, c’est-à-dire que P(x)-Q(x) est négligeable devant (x-x₀)ⁿ en x₀. Donc d’après la propriété 3 a₀=b₀, a₁=b₁,…, a_n=b_n. La fin est une autre conséquence de la propriété 3.

Propriété 5 : Si P et Q sont les développements limités à l’ordre n de f et g en x₀, alors le polynôme (P´Q)_x0,n troncature à l’ordre n en x₀ du produit P´Q (qui est un polynôme de degré pouvant aller jusqu’à 2n) est le développement limité de f´g à l’ordre n en x₀.

Démonstration :

Partons des hypothèses : Ecrivons que P et Q sont les DL_n(x₀) de f et g :

f(x)=P(x)+(x-x₀)ⁿe₁(x) et g(x)=Q(x)+(x-x₀)ⁿe₂(x)

On a alors :

(f´g)(x)=[P(x)+(x-x₀)ⁿe₁(x)][Q(x)+(x-x₀)ⁿe₂(x)]

=(P´Q)(x)+P(x)(x-x₀)ⁿe₂(x)+(x-x₀)ⁿe₁(x)Q(x)+(x-x₀)ⁿe₁(x)(x-x₀)ⁿe₂(x)

=(P´Q)(x)+(x-x₀)ⁿa(x)

avec a(x)=P(x)e₂(x)+Q(x)e₁(x)+(x-x₀)ⁿe₁(x)e₂(x) qui tend bien vers 0 en x₀ (les polynômes étant des fonctions continues, la limite est P(0)´0+Q(0)´0+0ⁿ´0´0=0).

Si T est la troncature (P´Q)_x0,n de (P´Q) à l’ordre n en x₀, on sait que (P´Q)(x)-T(x) est négligeable devant (x-x₀)ⁿ (cf. propriété 3), donc s’écrit b(x)(x-x₀)ⁿ où b(x) tend vers 0 en x₀.

Finalement :

(f´g)(x)=(P´Q)(x)+(x-x₀)ⁿa(x)

=T(x)+[(P´Q)(x)-T(x)]+(x-x₀)ⁿa(x)

=T(x)+(x-x₀)ⁿb(x)+(x-x₀)ⁿa(x)

=T(x)+(x-x₀)ⁿe(x)

avec e(x)=b(x)+a(x) qui tend vers 0+0=0 en x₀. Cette écriture prouve que T est bien le DL cherché.

Exemple : Calculer le DL d’ordre 2 en 0 de f(x)=e^xln(1+x).

On commence par écrire les DL à l’ordre 2 de e^x, et sin(x). On a [e^x]’=[e^x]’’=e^x, avec e0=1, par ailleurs [ln(1+x)]’=1/(x+1), [ln(1+x)]’’= -1/(x+1)², fonction qui valent 1 et -1. Finalement :

e^x=1+1´x+(1/2)´1´x²+x²e₁(x)=1+x+x²/2+x²e₁(x).

ln(1+x)=ln(1)+1´x+(1/2)´(-1)´x²+x²e₂(x)=x-x²/2+x²e₂(x)

On aura donc en multipliant ces deux égalités :

e^xln(1+x)=[1+x+x²/2+x²e₁(x)][x-x²/2+x²e₂(x)]

=x-x²/2+x²e₂(x)+x[x-x²/2+x²e₂(x)]+(x²/2)[x-x²/2+x²e₂(x)]+x²e₁(x)[x-x²/2+x²e₂(x)]

=x-x²/2+x²+x²[e₂(x)-x/2+xe₂(x)+(1/2)[x-x²/2+x²e₂(x)]+e₁(x)[x-x²/2+x²e₂(x)]]

=x+x²/2+x²e(x)

avec e(x)=e₂(x)-x/2+xe₂(x)+(1/2)[x-x²/2+x²e₂(x)]+e₁(x)[x-x²/2+x²e₂(x)], qui tend vers :

0-0/2+0´0+(1/2)[0-0²/2+0²´0]+0´[0-0²/2+0²´0]=0.

Donc on a bien obtenu le DL en 0 à l’ordre 2.

Une remarque qu’on peut faire, c’est que les termes qui contiennent x² fois d’autres termes en x, ou fois une fonction qui tend vers 0, seront de toutes façon négligeables à la fin, et qu’on peut les faire entrer directement dans un terme x²e(x), quitte à utiliser plusieurs lettres e, d, g, etc., en avançant le calcul. On peut ainsi se concentrer sur les termes qui doivent rester.

Une propriété plus fine est la suivante, très utile dans les calculs :

Propriété 6 : Soit f, g deux fonctions, définies dans des voisinages (pleins) du réel x₀ et de f(x₀)=y₀ respectivement. On suppose connus des développements limités P et Q de f et g en x₀ et y₀ respectivement, au même ordre n>0. Alors le polynôme R, obtenu en développant le polynôme composé QoP en fonction de (x-x₀) et en le tronquant à l’ordre n, est le développement limité de gof en x₀ à l’ordre n.

Démonstration : Là, pour écrire une preuve rigoureuse, on souffre… Beaucoup de lettres, beaucoup d’indices, beaucoup de calculs avec. Pour ajouter à l’inconfort, on va donc donner cette démonstration en petits caractères, réservés à ceux qui veulent vraiment la lire.

Il faut surtout retenir l’idée générale : comme une écriture de DL est une égalité,

f(x)=P(x)+(x-x₀)ⁿe(x),

on peut remplacer f(x) par P(x)+(x-x₀)ⁿe(x) et développer ceci dans les calculs. Si on obtient, au bout du compte, d’un côté un polynôme, et de l’autre une fonction qui peut s’écrire (x-x₀)ⁿ, fois une fonction tendant vers 0, on aura bien obtenu le DL.

La démonstration :

On suppose donc f(x)=P(x)+(x-x₀)ⁿe₁(x) où on remarque que P(x₀)=f(x₀)=y₀ d’après cette formule (car (x₀-x₀)ⁿe₁(x₀)=0ⁿe₁(x₀)=0). Par ailleurs g(y)=Q(y)+(y-y₀)ⁿe₂(y), et e₁(x) et e₂(y) tendent vers 0 quand x et y tendent vers x₀ et y₀ respectivement.

On suppose par ailleurs P et Q écrits en fonction de x-x₀ et y:

P(x)=a₀+a₁(x-x₀)+…+a_n(x-x₀)ⁿ, et Q(y)=b₀+b₁y+…+b_nyⁿ.

Alors gof(x)=g[f(x)]=Q(f(x))+(f(x)-y₀)ⁿe₂(f(x)). Examinons d’abord le dernier terme :

((f(x)-y₀)ⁿe₂(f(x))=(P(x)-y₀+(x-x₀)ⁿe₁(x))ⁿe₂(f(x)).

Or P(x₀)=y₀ donc le coefficient a₀ de P est égal à y₀, et :

P(x)-y₀=a₁(x-x₀)+…+a_n(x-x₀)ⁿ=(x-x₀)[a₁+…+a_n(x-x₀)^n-1]=(x-x₀)S(x)

où S est un nouveau polynôme, borné au voisinage de x₀ puisque tendant vers a₁. Finalement le terme étudié est égal à :

[(x-x₀)S(x)+(x-x₀)ⁿe₁(x)]ⁿe₂(f(x))=(x-x₀)ⁿ[S(x)+(x-x₀)^n-1e₁(x)]ⁿe₂(f(x))=(x-x₀)ⁿh(x)

avec h(x)=(S(x)+(x-x₀)^n-1e₁(x))ⁿe₂(f(x)) qui tend vers (a₁+0^n-1.0)ⁿ.0=0 car f(x) tend vers y₀ et e₂(y) tend vers 0 si y tend vers y₀. Donc ce terme est bien négligeable comme on le souhaitait.

Maintenant :

Q(f(x))=b₀+b₁f(x)+…+b_nf(x)ⁿ=b₀+b₁(P(x)+(x-x₀)ⁿe₁(x))+…+b_n(P(x)+(x-x₀)ⁿe₁(x))ⁿ.

Chaque terme b_k(P(x)+(x-x₀)ⁿe₁(x))^k peut se développer suivant des formules d’autant plus longues que k est grand, mais on aura des coefficients fois des termes :

P^k-j(x)(x-x₀)^nje₁^j(x)

On voit que (x-x₀)ⁿe₁(x) se met en facteur dès que j>0, et que l’autre facteur est une somme de fonctions du type b_kP^k-j(x)(x-x₀)^n(j-1)e₁^j-1(x) qui sont toutes bornées au voisinage de x₀. Finalement le seul terme dans lequel (x-x₀)ⁿe₁(x) n’est pas en facteur est b_kP^k(x), et on a :

Q(f(x))=b₀+b₁P(x)+…+b_kP^k(x)+…+b_nPⁿ(x)+(x-x₀)ⁿe₁(x)F(x), avec F bornée au voisinage de x₀. Autrement dit : Q(f(x))=Q(P(x))+(x-x₀)ⁿe₁(x)F(x), où e₁(x)F(x) tend vers 0 en x₀ puisque F est bornée.

En résumant l’ensemble du calcul on obtient :

gof(x)=Q(P(x))+(x-x₀)ⁿe₁(x)F(x)+(x-x₀)ⁿh(x)=QoP(x)+(x-x₀)ⁿe(x)

où e(x)=e₁(x)F(x)+h(x) tend vers 0 en x₀.

Donc gof-QoP est négligeable devant (x-x₀)ⁿ, et comme la troncature R de QoP à l’ordre n vérifie que QoP-R est négligeable devant (x-x₀)ⁿ par la propriété 3, on en déduit que R est bien le développement limité de gof.

Exemple : calculer le DL à l’ordre 2 en 0 de ln(cos(x)).

On a cos(0)=1, donc on va devoir composer le DL à l’ordre 2 de cos(x) en 0 et le DL à l’ordre 2 en 1 de ln(x).

Comme cos’(x)= -sin’(x), qui vaut 0 en 0, et cos’’(x)=-cos(x), qui vaut -1 en 0, on a :

cos(x)=1+0x+(1/2)(-1)x²+x²e₁(x)=1-x²/2+x²e₁(x) ;

et comme ln’(y)=1/y, ln’’(y)= -1/y², on a ln’(1)=1, ln’’(1)= -1, et :

ln(y)=ln(1)+1(y-1)+(1/2)(-1)(y-1)²+(y-1)²e₂(y)=(y-1)-(y-1)²/2+(y-1)²e₂(y).

on peut donc composer :

ln(cos(x))=(cos(x)-1)-(cos(x)-1)²/2+(cos(x)-1)²e₂(cos(x))

=[1-x²/2+x²e₁(x)-1]-[1-x²/2+x²e₁(x)-1]²/2+[1-x²/2+x²e₁(x)-1]²e₂(cos(x))

Et on développe, en négligeant d’emblée les termes en x2 fois quelque chose qui tend vers 0 :

=[-x²/2+x²e₁(x)]-[-x²/2+x²e₁(x)]²/2+[-x²/2+x²e₁(x)]²e₂(cos(x))

= -x²/2+x²e₁(x)-x²[-x/2+xe₁(x)]²/2+x²[-x/2+xe₁(x)]²e₂(cos(x))

= -x²/2+x²e(x).

Tous les termes sont négligeables sauf le premiers, on a finalement :

ln(cos(x))= -x²/2+x²e(x).

On peut donc composer, multiplier, etc., les développements limités. Pour simplifier un peu les calculs, on peut remarquer que les développements limités en 0 suffisent, car on peut toujours se ramener à ce cas-là.

Propriété 7 : Le polynôme P est un développement limité à l’ordre n de la fonction x a f(x) au voisinage de x₀ si et seulement si le polynôme R(h)=P(x₀+h) est un développement limité en 0 à l’ordre n de la fonction h af(x₀+h).

Démonstration : La première propriété s’écrit : il y a une fonction qui tend vers 0 en x₀ telle que f(x)=P(x)+(x-x₀)ⁿe(x), et la seconde s’écrit : il y a une fonction tendant vers 0 en 0 telle que f(x₀+h)=P(x₀+h)+hⁿh(h). Il est donc clair qu’on peut passer d’une formule à l’autre avec h(h)=e(x₀+h) ou e(x)=h(x-x₀).

Les calculs sont en général plus simples en 0, les termes en h^k étant plus simples à gérer que les (x-x₀)^k. On pourra s’entraîner à re-démontrer les propriétés de calcul dans ce cas-là.

Voyons une dernière propriété de calcul.

Propriété 8 : (Développement limité et dérivation) On se donne a un réel, toutes les fonctions considérées sont définies dans un même voisinage de a.

1) Soit f une fonction dérivable, telle que f(a)=0 et que f’ admette un développement limité nul à l’ordre n en a : f(x)=(x-a)ⁿe₁(x) avec e₁(x)=0. Alors f(x) admet un développement limité nul à l’ordre n+1 en a.

2) Soit f une fonction dérivable, et P le développement limité à l’ordre n en a de f’. On suppose que Q est un polynôme tel que Q’=P et Q(a)=f(a). Alors Q est le développement limité à l’ordre (n+1) de f en a.

Autrement dit : si f’(x)=a₀+a₁(x-a)+…+a_n(x-a)ⁿ+(x-a)ⁿe(x) avec e(x)=0, alors il existe une fonction h telle que f(x)=f(a)+a₀(x-a)+(x-a)²+…+(x-a)ⁿ⁺¹+(x-a)ⁿ⁺¹h(x) avec h(x)=0.

Démonstration :

Ces propriétés tournent autour de la même idée rencontrée pour démontrer la formule de Taylor Young, à savoir qu’une fonction dont la dérivée s’écrit (x-x₀)ⁿ fois une fonction qui tend vers 0, sera du type (x-x₀)ⁿ⁺¹ fois une fonction qui tend vers 0. On a simplement à appliquer judicieusement le théorème des accroissements finis, mais comme one ne traite pas ici de la « vraie » définition de la limite, on ne rédigera pas ces démonstrations.

Quelques exemples aideront à comprendre l’usage habituel et le calcul des DL.

Exemples :

- Trouver le DL de f(x)=e^sin(x) en 0 à l’ordre 3. D’après la formule de Taylor-Young on a e^x=1+x+x²/2+x³/6+x³a(x) avec a tendant vers 0 en 0, et sin(x)=x-x³/6+x³b(x)=x+x²c(x) avec b,c tendant vers 0 en 0. On peut donc écrire :

e^sin(x)=1+(x-x³/6+x³b(x))+(x+x²c(x))²/2+(x+x²c(x))³/6+x³a(x)(1+xc(x))³

On a choisi un développement plus réduit de sinus pour les termes en sin²(x) et sin³(x) car en les développant, dès qu’on multiplie un terme x²c(x) par un terme en x, on a du x³c(x) qui sera négligeable dans le développement final. On voit donc qu’il suffit d’aller à l’ordre 2 dans les termes d’ordre >1 du développement de l’exponentielle. On obtient :

(x+x²c(x))²/2=x²/2+x³c(x)+x⁴c(x)/2=x²/2+x³d₁(x) où d₁ tend vers 0 en 0.

(x+x²c(x))³/6=x³/6+3x².x²c(x)/6+3x.x⁴c²(x)/6+x⁶c³(x)/6=x³/6+x³d₂(x) avec d₂ tendant vers 0 en 0.

En additionnant tout ceci il vient :

e^sin(x)=1+x-x³/6+x²/2+x³/6+x³(b(x)+d₁(x)+d₂(x))=1+x+x²/2+x³e(x).

On a donc trouvé le DL d’ordre 3 de f(x) en 0, c’est le polynôme 1+x+x²/2. Dans les calculs, on voit qu’on peut simplifier les notations et n’écrire que les termes en x,x²,x³ (pour l’ordre 3) ou les termes constants : les autres termes rentrent tous dans une grande parenthèse x³e(x) où on pourrait écrire précisément comme somme de fonctions déjà introduites, mais cela n’a pas d’intérêt, on sait de toute façon que e tendra vers 0 en 0, les propriétés 7 et 9 nous l’assurent.

- Soit f(x)=e^sin(x). Trouver f’’(0) et f⁽³⁾(0) :

On a vu le DL de f à l’ordre 3, f(x)=1+x+x²/2+x³e(x), or f est indéfiniment dérivable comme composée de fonctions indéfiniment dérivables, donc la formule de Taylor-Young est valable, et f(x)=f(0)+xf’(0)+x²f’’(0)/2+x³f’’’(0)/6+x³h(x). Comme le DL à l’ordre 3 est unique, on a forcément f’’(0)/2=1/2, f’’’(0)/6=0, ce qui donne f’’(0)=1, f’’’(0)=0.

- Trouver la limite de (e^sin(x)-e^x)/x³ quand x tend vers 0.

On utilise les DL connus : e^sin(x)=1+x+x²/2+x³e(x), e^x=1+x+x²/2+x³/6+x³a(x), ce qui donne par soustraction e^sin(x)-e^x=-x³/6+x³d(x) avec d(x)=e(x)-a(x) tendant vers 0 en 0. Donc on a (e^sin(x)-e^x)/x³= -1/6+d(x) tend vers –1/6+0=-1/6 quand x tend vers 0.

On voit donc que les DL peuvent être utilisés pour de nombreuses situations : limites à calculer, nombres dérivés n-èmes à estimer en certains points, etc.

On prendra garde toutefois, pour ce qui concerne les nombres dérivés : il n’y a pas de réciproque à la méthode ci-dessus. Si f admet un DL en 0, elle n’est pas forcément n fois dérivable, même pour n=2.

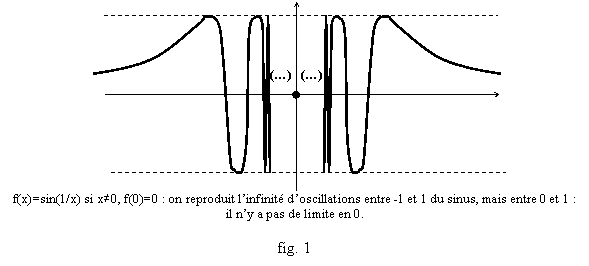
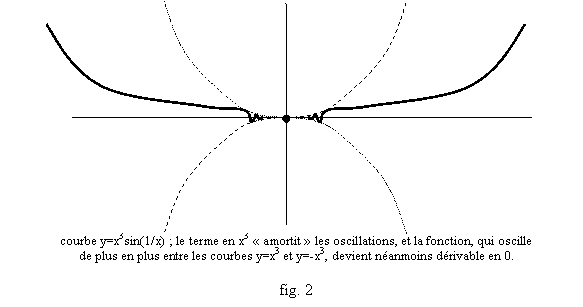
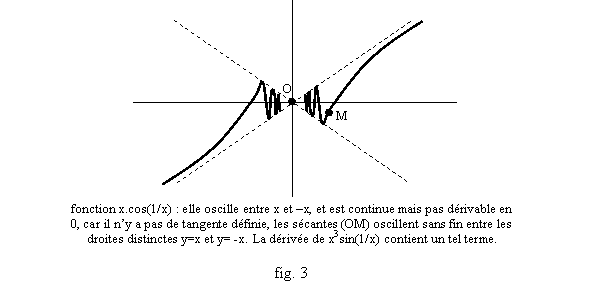
Soit f(x)=x³sin(1/x) pour x¹0 et f(0)=0. Alors f est continûment dérivable sur R puisque si x¹0, f’(x)=3x²sin(1/x)-x.cox(1/x) qui tend vers 0 en 0, et (f(x)-f(0))/x=x²sin(1/x) tend vers 0 en 0 donc f’(0)=0. Mais f’(x)/x=3x.sin(1/x)-cos(1/x) n’a pas de limite quand x®0, donc f’’(0) n’existe pas. Or f est indéfiniment dérivable sur R* et admet donc en tout x₀¹0 un DL de tout ordre, et f admet un DL d’ordre 2 en 0 puisque f(x)=0+x²a(x) avec a(x)=x.sin(1/x) tendant vers 0 en 0. On peut retenir le graphe de ce type de fonctions, qui fournissent des contre-exemples à beaucoup de propriétés (fig. 1, 2, 3).

Autre utilisation possible des DL : les inégalités. Si on a un DL comme celui de f(x)=e^sin(x), f(x)=1+x+x²/2+x³e(x). Alors on peut comparer f(x) et une de ses approximations, comme 1+x : f(x)-1-x=x²(1/2+x.e(x)). La fonction entre parenthèse tend vers 1/2 quand x tend vers 0, donc il y a un voisinage ]-r,r[ de 0 où f(x)-1-x est du signe de x², c’est-à-dire positif. De plus il est non nul si x¹0. On a donc un intervalle autour de 0 où f(x)>1+x si x¹0. On peut préciser la position de f(x) par rapport à 1+x+x²/2 en allant chercher le terme suivant du DL, cx³ si le c correspondant est non nul, ou plus loin.

La limite de cette méthode est qu’on ne connaît pas l’intervalle ]-r,r[ où l’inégalité est vraie. Pour des résultats plus précis, il faut faire des études de fonctions ou utiliser des résultats du type accroissements finis.

On ne voit pas ici comment calculer le DL d’un quotient f(x)/g(x) en 0 par exemple, si g(0)¹0. On ne dispose pas ici des techniques algébriques nécessaires de calculs sur les polynômes. Mais on peut heureusement réussir sans ces techniques.

Une première méthode est de voir l'inversion comme une composition : on calcule le DL au voisinage de g(0)¹0 de X a 1/X, et on compose ce DL et celui de g pour trouver au voisinage de 0 le DL de x a1/g(x), et enfin on multiplie par le DL de f(x). On a des illustrations de cette méthode dans les exercices.

Une autre méthode est l’identification : on considère les coefficients du DL de f(x)/g(x), à l’ordre voulu, mettons l’ordre 2, comme des inconnues a₀, a₁, a₂. Ainsi f(x)/g(x)=a₀+a₁x+a₂x²+x²e(x). Comme on connaît le DL de g(x)=b₀+b₁x+b₂x²+x²a(x) et de f(x)=c₀+c₁x+c₂x²+x²b(x), et que f(x)=(f(x)/g(x)).g(x), on doit avoir, d’après les propriétés des opérations sur les DL, (c₀+c₁x+c₂x²)=[(a₀+a₁x+a₂x²)(b₀+b₁x+b₂x²)]_0,2 ce qui donne, en identifiant les coefficients (unicité, propriété 3), des équations qui permettent de trouver a₀, a₁, a₂. Cette méthode ne doit être employée que si on sait déjà que le DL existe, pour le calculer. Par exemple si les fonctions sont indéfiniment dérivables. En effet on ne démontre pas ici que le DL existe contrairement à la méthode qui utilise la composition des fonctions.

Exemples : Trouver le DL en 0 à l’ordre 2 de sin(x)/(1+sin(x)).

1^ère méthode : comme 1+sin(0)=1, on cherche le DL de 1/u en u₀=1 à l’ordre 2. Comme les dérivées premières et seconde de 1/u sont –1/u² et 2/u³ qui valent –1 et 2 en 1, on trouve par la formule de Taylor Young 1-(u-1)+(u-1)² comme DL à l’ordre 2. Autrement dit :

1/u=1-(u-1)+(u-1)²+(u-1)²a(u)

avec a(u) tendant vers 0 quand u tend vers 1. Donc :

1/(1+sin(x))=1-((1+sin(x))-1)+((1+sin(x))-1)²+((1+sin(x))-1)²a(1+sin(x))

=1-sin(x)+sin²(x)+sin²(x)a(1+sin(x)).

(on peut aussi écrire le DL en 0 : 1/(1+h)=1-h+h²+h²a₁(h), et appliquer ceci à h=sin(x). C’est toujours légitime, pour que cela soit efficace, il faut l’appliquer à une fonction comme sin(x) qui tend vers 0 en 0 : ainsi a₁(sin(x)) tendra vers 0 quand x tend vers 0 et l’écriture obtenue :

1/(1+sin(x))=1-sin(x)+sin²(x)+sin²(x)a₁(sin(x))

permettra bien d’obtenir un DL).

Maintenant on sait que sin(x)=x+x²b(x) avec b tendant vers 0 en 0. Donc on peut écrire :

1/(1+sin(x))=1-(x+x²b(x))+(x+x²b(x))²+(x+x²b(x))²a(1+sin(x))

=1-x+x²-x²b(x)+2x³b(x)+x⁴b²(x)+x²(1+xb(x))²a(1+sin(x))

=1-x+x²+x²c(x) avec c(x)=-b(x)+2xb(x)+x²b²(x)+(1+xb(x))²a(1+sin(x))

qui tend vers -0+2.0.0+0².0²+(1+0.0)².0=0 quand x tend vers 0. Le DL de 1/(1+sin(x)) est donc 1-x+x².

Pour trouver celui de sin(x)/(1+sin(x)) il suffit de multiplier par le DL de sin(x)=x+x²b(x), on trouve [x.(1-x+x²)]_0,2=[x-x²+x³]_0,2=x-x² qui est le DL cherché.

2^ème méthode : Posons sin(x)/(1+sin(x))=a₀+a₁x+a₂x²+x²d(x). Comme on a sin(x)=x+x²b(x), on a aussi 1+sin(x)=1+x+x²b(x) et donc sin(x)=[sin(x)/(1+sin(x))](1+sin(x)) donne pour les DL que :

x=[(a₀+a₁x+a₂x²)(1+x)]_0,2

soit

x=[a₀+(a₀+a₁)x+(a₁+a₂)x²+…]_0,2=a₀+(a₁+a₀)x+(a₁+a₂)x².

Donc on a les équations a₀=0, a₀+a₁=1, a₁+a₂=0, ce qui donne a₀=0, a₁=1, a₂=-1. Le DL cherché est donc x-x².

Pour simplifier le travail de calcul dans bien des problèmes, il vaut mieux connaître par cœur un certain nombre de développements limités de fonctions usuelles. On tire ces développements de la formule de Taylor-Young, et des dérivées des fonctions usuelles :

· e^x est sa propre dérivée n-ème,

· sin(x) et cos(x) ont leur dérivées qui passent par les valeurs cos(x), -sin(x), -cos(x), sin(x) toutes les 4 fois.

· ln(x) a pour dérivée 1/x, pour dérivée seconde –1/x², pour dérivée 3^ème 2/x3, puis 2(-3)/x⁴, puis 2.3.4/x⁵, etc. Sa dérivée n-ème est (-1)^n-1(n-1)!/xⁿ,

· la dérivée (n-1)-ème de 1/x, soit (1/x)⁽ⁿ⁾=(-1)ⁿn !/xⁿ⁺¹. On a donc :

On obtient ainsi les DL suivants :

en 0 :

(ordre n).

(ordre 2n+2)

(ordre 2n+1)

en 1 :

.

.

ou, si on préfère en 0 :

.

.

Dans ces écritures, les fonctions a, b, c, e, h, tendent vers 0 en 0, et les fonctions d et e tendent vers 0 quand x tend vers 1.

Le DL de 1/x en 1 ou de 1/(1+h) en 0 sont ceux qu’on utilisera souvent pour calculer des DL de quotients. Ils sont donc à connaître absolument.

Exercices :

1) Calculer les développements limités en 0 à l’ordre n indiqué des fonctions suivantes :

f(x)=cos(sin(x)), n=3 ; g(x)=sin(cos(x)), n=3 ; h(x)=tan(x), n=3 ; i(x)=ln(cos(e^x-1)), n=2.

2) Trouver les DL des fonctions suivantes aux points a indiqué et à l’ordre n indiqué :

f(x)=sin(x), a quelconque, n=3 ; g(x)=ln(x), a=1, ordre n ; h(x)=(x²-1)/(x²+1), a=1, n=3.

3) Montrer que si f est une fonction paire et admet un DL_n(0), ce DL ne contient que des termes d’exposants pairs. Si f est impair, il n’y aura que des termes d’exposants impairs.

4) Calculer les limites suivantes à l’aide de DL :

; ; .

5) Soit f(x)=x^x pour x>0.

a) Montrer que f peut être prolongée par continuité en 0. On note encore f ce prolongement.

b) Montrer que pour tout n il y a une fonction e tendant vers 0 en 0 telle que, pour tout x>0 :

f(x)=1+x.ln(x)+(1/2)x².ln²(x)+…+(1/n !)xⁿ.lnⁿ(x)+xⁿ.lnⁿ(x).e(x).

c) f est-elle dérivable à droite en 0 ? Admet-elle des DL en 0 ? A quels ordres ?

6) Montrer que la fonction f(x)=x²ⁿ⁺¹cos(1/xⁿ) est continûment dérivable sur R, admet un DL d’ordre 2n en 0, mais que f’(x) n’a même pas un DL d’ordre 1 en 0.

7)

a) Donner le DL à l’ordre n en 0 de (1+x)^a, où a est un réel fixé.

b) Quels sont les DL à l’ordre n en 0 de  ?

8) Soit f une fonction définie dans un intervalle ]-r,r[ (avec r>0). On suppose f dérivable en 0 avec f'(0)=a¹0. Prouver que f admet un DL ax+bx² d'ordre 2 en 0 si et seulement si existe et est un réel l. Quel rapport y a-t-il alors entre l et b ? Applications : calculer ; .

9) Soit f(x)=e^-1/|x| si x¹0, f(0)=0.

a) Montrer que f est indéfiniment dérivable sur R^*.

b) Montrer qu’il y a pour tout n un polynôme P_n tel que :

f⁽ⁿ⁾(x)=P_n(x)/x²ⁿe^-1/|x| si x>0, et f⁽ⁿ⁾(x)=(-1)ⁿP_n(|x|)/x²ⁿe^-1/|x| si x<0.

c) Montrer que f est indéfiniment dérivable sur R.

d) Quel est le DL de f en 0 à l’ordre n ?

10) Peut-on choisir a,b pour que le rapport [a.sin(x)+b.x.cos(x)]/x³ tende vers 1 quand x tend vers 0 ? Et a,b,c tels que [a.sin(x)+b.tan(x)+c.Arctg(x)]/x³ tend vers 2 si x tend vers 0 ?

11) Soit f une fonction définie dans un intervalle ]-r,r[ (avec r>0) et nÎN* un naturel fixé. On suppose f dérivable en 0 avec f'(0)=a¹0. On considère par ailleurs un polynôme P tel que P(0)=0 et deg(P)£n. Prouver que existe et est un réel l si et seulement si les deux conditions suivantes sont satisfaites : 1) P est le DL d'ordre n de f en 0 ; 2) f a un DL d'ordre n+1 en 0. Si ces conditions sont vérifiées, calculez le DL d'ordre n+1 de f en 0 en fonction de P et l. Application : calculez .