Mathématiques

Cours-TD – Culture Scientifique de base – 2005-2006

Chapitre 2 - Dérivées des fonctions de R dans R. Applications. Fonctions élémentaires

À partir de ce chapitre, toutes les propriétés, toutes les affirmations sur les fonctions – et le reste – seront, autant que possible, justifiées par des démonstrations. Pourquoi ? Dans les sciences expérimentales on établit des lois générales (relation fondamentale de la dynamique, etc.), qui expliquent ainsi le principe de cause à effet. En mathématique, les objets étudiés sont des outils de calculs abstraits, avec pour seule contrainte leur logique interne (exprimées dans les règles de calculs, par exemple). Conséquence : les relations de cause à effet, qu’on peut vérifier dans la nature, pour les autres sciences, par des expériences, ne peut se vérifier en mathématique qu’en écrivant une démonstration, un texte où la conclusion souhaitée apparaît comme la conséquence obligatoire des hypothèses de départ. Rien ne doit être accepté en mathématique sans démonstration car, dans le domaine de l’abstrait, on peut « tout imaginer », même des contre-exemples improbables aux affirmations qui ont l’air le plus vraies. Par ailleurs, une démonstration abstraite permet aux règles de calcul et outils mathématiques de s’appliquer indépendamment du contexte, à toutes les situations et tous les problèmes même très différents.

Dans le premier chapitre, on a donné des propriétés, compliquées à prouver, et même à définir (limite, continuité, etc.), sans les justifier, parce que cela aurait pris bien du temps et nécessite de longs travaux : on les admet donc, et on pourra les utiliser. Mais dans la suite, sauf cas exceptionnel, on prouvera que chaque nouvelle propriété est conséquence des précédentes, et on attend des étudiants qu’ils fassent de même face à un exercice : qu’ils justifie tout ce qu’ils affirment, en s’appuyant sur les propriétés vues en cours, en cherchant à « convaincre » le lecteur – le correcteur – que ce qui est affirmé est vrai.

1) – Définition de la dérivation

Définition : Soient f une fonction, définie sur l’intervalle I, et a un élément de I. On dit que f est dérivable au point a si le rapport (f(x)-f(a))/(x-a) a une limite l quand x tend vers a. Dans ce cas cette limite l est appelée alors nombre dérivé de f en a. On note l=f’(a), ou encore l=. S’il y a une limite à gauche ou à droite on parle de dérivée à gauche ou à droite. On note f’_g(a) et f’_d(a) ces limites.

Calculer une dérivée d’une fonction en un point, c’est lever une indétermination puisque x-a tend vers 0 quand x tend vers a, et f(x)-f(a) aussi quand la fonction est continue (la différence tend vers f(a)-f(a)=0), donc le quotient se présente sous la forme indéterminée 0/0.

Exemples : dérivées de fonctions usuelles :

Dérivée d’une fonction constante. Posons f(x)=C constante, et fixons un réel a. Pour tout x¹a, on a :

le rapport est donc toujours égal à 0, et quand x tend vers a, la limite vaudra 0. La dérivée existe en tout point a et on a f’(a)=0.

Considérons deux nombres u et v fixés d’avance, et f(x)=ux+v, la fonction affine de coefficient directeur u et de coefficient à l’origine v ; soit a un réel, et x un réel différent de a. On peut alors calculer la différence :

f(x)-f(a)=[ux+v]-[ua+v]=[ux-ua]+[v-v]=u(x-a).

Donc, si on divise par x-a, on obtiendra :

et comme le rapport est toujours égal à u, quand x tend vers a, sa limite reste égale à u. donc quel que soit a, la dérivée existe, et vaut : f ’(a)=u.

Remarque : en particulier si u=1, v=0, on obtient la fonction f(x)=1x+0=x, c’est-à-dire f=Id, et donc la dérivée vaut 1 en tout point a :

Id’(a)=1.

Considérons la fonction f(x)=1/x, définie sur R^*, et soit a un réel fixé non nul. Prenons x¹a, et effectuons le calcul :

 ;

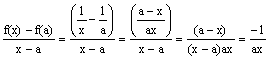quand x tend vers a, d’après les théorèmes donnant les règles de calculs des limites, l’expression -1/(ax) tend vers -1/a². Ainsi, quel que soit a¹0, la fonction f est dérivable en a et on a : f ’(a)= -1/a² :

Considérons maintenant définie sur R₊. Fixons a≥0, et x un réel positif mais différent de a. On peut encore effectuer le calcul :

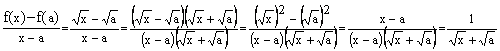
Cette technique pour éliminer des différences de racines difficiles à simplifier par des sommes s’appelle « multiplier par la quantité conjuguée », et ici on a juste multiplié en haut et en bas par le bon nombre ; il faut juste que ce nombre soit non nul puisque comme a et x sont distincts, l’un des deux au moins est non nuls, donc la somme de leurs racines carrées est strictement positive.

Une fois ce calcul effectué, les calculs habituels de limites prouvent que tend vers quand x tend vers a. Si a est non nul, cette limite est non nulle, et l’inverse tend donc vers , et on a f ’(a)=. En revanche si a=0, =0, donc le réel positif tend vers 0, et son inverse tend vers +∞ : f n’est pas dérivable en 0.

.

Dernier exemple : on fixe un entier naturel n non nul, et on étudie la fonction puissance f(x)=xⁿ ; choisissons a un réel quelconque et x¹a. On a la factorisation, vue au chapitre 1 :

f(x)-f(a)=xⁿ-aⁿ=(x-a)(x^n-1+x^n-2a+…+xa^n-2+a^n-1),

donc, si x¹a on aura :

[f(x)-f(a)]/(x-a)=x^n-1+x^n-2a+…+xa^n-2+a^n-1.

C’est l’expression d’une fonction continue en tout point, de limite en x=a égale à

a^n-1+a^n-2a+…+aa^n-2+a^n-1=na^n-1.

On en déduit que f est dérivable en a, avec f’(a)=na^n-1.

Tous ces exemples pour souligner qu’il faut se familiariser avec les calculs de taux de variations, les simplifications permettant de lever ces indéterminations. Maintenant on peut aussi se reporter, dans la pratique, à ces fonctions « de base » vues ci-dessus, et aux théorèmes permettant de calculer la dérivée d’une somme, d’un produit, etc.

Propriété 1 : f,g, désignent des fonctions, a un réel, etc.

a. Si f est dérivable en a elle est continue en a.

b. Si f, g sont dérivables en a et si a,b sont réels, alors (a.f+b.g) est dérivable en a et son nombre dérivée y est a.f’(a)+b.g’(a). De même (f´g) est dérivable en a de nombre dérivée f’(a)g(a)+g’(a)f(a). Si g(a)¹0, (f/g) est aussi dérivable en a, de nombre dérivé (f’(a)g(a)-g’(a) f(a))/g(a)².

c. Si f est dérivable en a, f(a)=b, et si g est dérivable en b, alors g°f est dérivable en a de nombre dérivé g’(b)×f’(a) (autrement dit (g°f)’(a)=g’(f(a))f’(a)).

Démonstration :

a. En effet f(x)-f(a)=[(f(x)-f(a))/(x-a)]´(x-a) tend alors vers f’(a)´0=0 quand x tend vers a, c’est-à-dire que f(x) tend vers f(a).

b. On utilise les propriétés des opérations sur les limites : pour tout x¹a, notons T_f(x) et T_g(x) les taux d’accroissement (f(x)-f(a))/(x-a) et (g(x)-g(a))/(x-a). Les fonctions étant dérivables, ces taux ont des limites l, l’ quand x tend vers a. Alors pour x¹a :

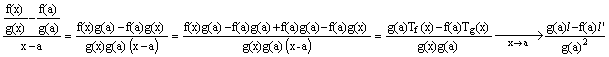
pour les deux dernières limites, on a utilisé le a. : comme f et g sont dérivables, elles sont continues donc g(x) tend vers g(a) quand x tend vers a.

c. Posons R(y)= si y¹b, et R(b)=R(f(a))=g’(b). R est continue en b par définition du nombre g’(b) : c’est le prolongement par continuité de T_g. On peut écrire :

Si f(x)¹f(a),

Si f(x)=f(a), et , donc on a encore :

On a donc pour tout x¹a, .

Une façon un peu différente de voir la dérivée, parfois utile, est la suivante :

Propriété 2 : Soit f une fonction définie dans un voisinage de a et l un réel ; alors les propriétés suivantes sont équivalentes :

§ f est dérivable en a et f’(a)=l.

§ (f(a+h)-f(a))/h tend vers l quand h tend vers 0.

§ Il existe une fonction x ae(x) telle que e(x) tend vers 0 quand x tend vers a, et telle que f(x)=f(a)+(x-a)(l+e(x)).

§ Il existe une fonction h ae(h) telle que e(h) tend vers 0 quand h tend vers 0, et telle que f(a+h)=f(a)+h(l+e(h)).

Démonstration : l’équivalence des deux premières est une propriété générale des limites vue dans le chapitre précédent (changement de variable h=x-a ou x=a+h), tandis que les deux dernières sont aisées puisque cela revient par exemple à écrire (f(a+h)-f(a))/h=l+e(h) et dire que le rapport tend vers l revient alors à dire que e(h) tend vers 0.

Remarque :

§ les écritures ci-dessus s’appellent « développement limité de f à l’ordre 1 en a », ou «  de f(a+h) à l’ordre 1 en 0 ».

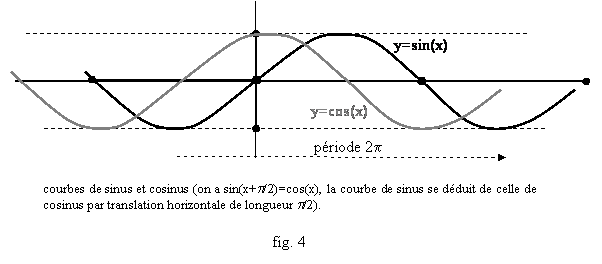
§ On comprend mieux, avec elles, l’interprétation géométrique de la dérivation : la dérivée est la pente de la tangente, autrement dit la tangente au point (a,f(a)) au graphe de f est la droite d’équation y=f(a)+f’(a)(x-a). Précisons ces notions : pour une fonction comme f(x)=x² (fig. 1), f(x)=x³, …, il semble intuitif que l’axe horizontal est tangent à la courbe en a=0. En revanche les fonctions linéaires, dont la courbe est une droite y=kx, coupent cet axe, si k¹0. Ce n'est pas seulement que la différence f(x)-kx change de signe : c'est toujours le cas, même pour la tangente, si f(x)=x³ par exemple (fig 2).

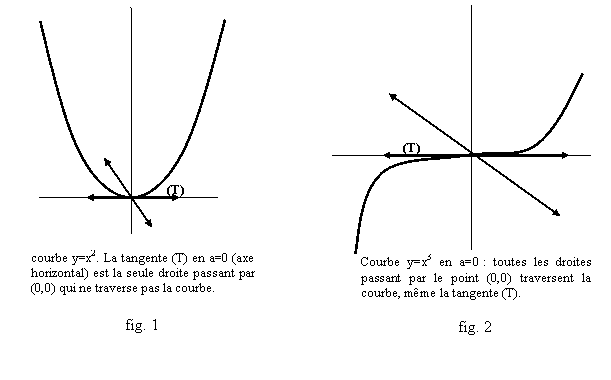
Par "traverser", il faut comprendre que la droite et la courbe font un angle - ce qui est une notion géométrique. Ceci peut être exprimée de manière un peu impressionniste, en disant que la fonction y=f(x), telle que f(0)=0, doit passer bien en dessous de chaque droite y=kx quand x tend vers 0. Ceci peut s’exprimer par une limite : f(x)/x doit être en valeur absolue inférieur à tout k quand x tend vers 0, autrement dit tendre vers 0, c’est-à-dire qu’on doit avoir f’(0)=0. Semblablement on pourra considérer que la droite y=k.(x-a)+f(a) est tangente à la courbe de f au point (a,f(a)) si la différence f(x)-f(a)-k(x-a) est bien plus petite que toute fonction linéaire nulle en a, ou que [f(x)-f(a)-k(x-a)]/(x-a) est inférieure à tout nombre fixé d’avance non nul, autrement dit si [f(x)-f(a)]/(x-a) tend vers k.

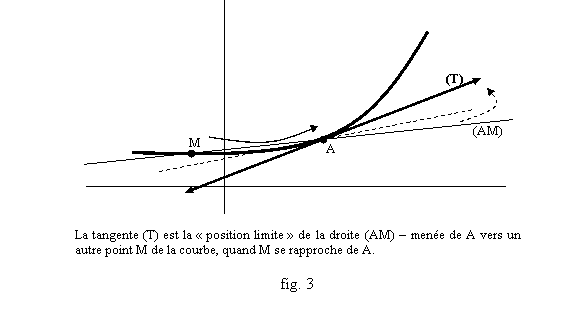
§ Une autre façon de le voir est de remarquer que (f(x)-f(a))/(x-a) est la pente, ou le coefficient directeur, de la droite joignant les points A(a,f(a)) et M(x,f(x)) de la courbe. Quand x tend vers a, M se rapproche de A et si le coefficient directeur de la droite tend vers un réel fixe k, c’est que la droite elle-même se rapproche de la droite passant par A et de coefficient directeur k (fig 3). C’est bien l’idée qu’on se fait d’une tangente.

§ Il y a une troisième façon de le voir, plus "calculatoire". Supposons un instant que le lecteur connaisse les fonctions trigonométriques : sinus, cosinus, tangente, qui permettent d’étudier les angles (cf. fin du chapitre, fonctions trigonométriques). Posons D(x)=(f(x)-f(a))/(x-a). On sait que le vecteur U de composantes (x-a, f(x)-f(a)) dirige la droite (AM), tandis que le vecteur (1,k) dirige la droite de coefficient directeur k passant par A. Les

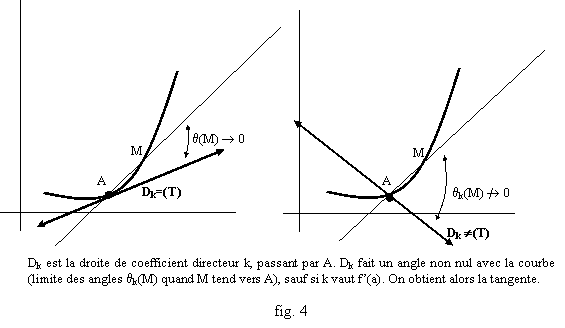
formules classiques du plan donnent comme valeur du sinus de l’angle (AM, u) le nombre [(x-a)k- (f(x)-f(a))]/P(x) et pour le cosinus [(x-a)+k(f(x)-f(a))]/P(x), où P(x) est la norme du vecteur U, P(x)=((x-a)²+(f(x)-f(a))²)^1/2(1+k²)^1/2. Ceci donne une valeur de la tangente : T(x)=[(x-a)k-(f(x)-f(a))]/[(x-a)+k(f(x)-f(a))]=[k-D(x)]/[1+kD(x)]. Si D(x) tend vers un réel l, T(x) tendra vers (k-l)/(1+kl), nul si et seulement si k=l. Le cas kl=-1 donne une limite infinie pour |T(x)| donc un angle de ±p/2. Si k=l la tangente tend vers 0, donc la droite de coefficient directeur l passant par A est la « position limite des droites (AM) ». Réciproquement si l’angle tend vers 0, sa tangente T(x) aussi. Or : T(x)=[k-D(x)]/[1+kD(x)] Û D(x)=(k-T(x))/[1+kT(x)] ; donc si T(x) tend vers 0, D(x) tend vers (k-0)/(1+k.0)=k. Ainsi l’angle entre (AM) et la droite de coefficient directeur k et passant par A tend vers 0 quand x tend vers a si et seulement si f est dérivable en a et f’(a)=k (fig 4). Remarque : voir dans le chapitre 2 les rappels sur les fonctions trigonométriques.

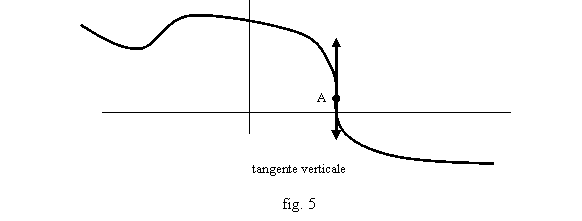
§ Dans cette ordre d’idée si (f(x)-f(a))/(x-a) tend vers ±¥ quand x tend vers a, on considère que la droite « verticale » d’équation x=a est tangente à la courbe au point A. La limite des angles est toujours 0, mais le calcul doit être effectué avec le vecteur directeur (0,1). On trouve T(x)=1/D(x) qui tend bien vers 0 si D(x) tend vers ±¥, ou simplement si |D(x)| tend vers +¥ (fig 5).

§ On notera que l’existence de la dérivée est un calcul de forme indéterminée puisque les fonctions concernées étant continues, [f(x)-f(a)]/(x-a) est de la forme 0/0. Les tables de dérivées nous fournissent donc un certain nombre de limites de références pour lever les indéterminations.

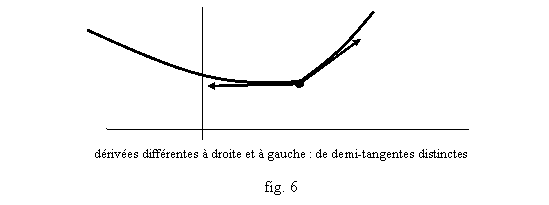
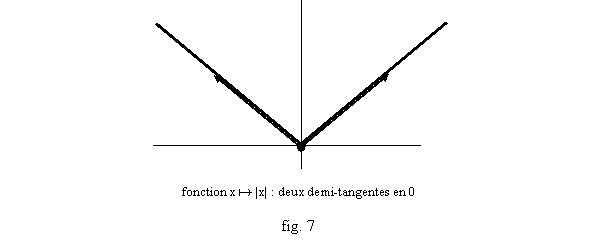
§ Quand une fonction a une dérivée seulement à gauche ou à droite en un point, on parle de demi-tangente à gauche ou à droite au graphe, avec le coefficient directeur correspondant. Certaines fonctions peuvent ne pas être dérivable mais avoir une dérivée à gauche et à droite (fig 6 ou la fonction valeur absolue, fig. 7). Si une fonction f a une dérivée à gauche et à droite en a, comme pour n'importe quelle limite, elle est dérivable en a si et seulement si f'_g(a)=f'_d(a), et cette valeur commune est alors f'(a).

La dérivée est surtout utilisée comme propriété globale, de même qu’on étudie peu les fonctions continues en un point, mais beaucoup celles continues sur tout un intervalle.

Définition : une fonction f définie sur un intervalle I est dérivable si elle est dérivable en tout point de I. L’application f’ qui à tout x de I associe le nombre dérivé f’(x) en x s’appelle alors fonction dérivée de f.

Propriété 3 :

a. Si f est dérivable sur I elle est continue sur I.

b. Si f et g sont des fonctions dérivables sur un intervalle I, alors pour tous réels a et b, la combinaison a.f +b.g est dérivable, avec (a.f+b.g)’=a.f’+b.g’, ainsi que f´g avec (f´g)’=f’´g+f´g’. Si g ne s’annule pas sur I, (f/g) est dérivable avec (f/g)’=(f’´g-f´g’)/g².

c. Si f est dérivable sur I, telle que f(I)ÍJ, et si g est dérivable sur J, alors g°f est dérivable sur I et (g°f)’=(g’°f)´f’.

Démonstration : on applique juste la propriété 1 en tout point de I.

Quelques applications de ces règles de calcul :

Posons f(x)=xⁿ. On peut utiliser les calculs de dérivations des fonctions composées pour calculer, si g est dérivable, la dérivée de la fonction f°g=gⁿ :

(f’°g)g’=n(g)^n-1g’=ng’g^n-1.

Autre application, la dérivée d’un polynôme P :

P(x)=a₀+a₁x+a₂x²+...+a_kx^k+...+a_nxⁿ.

D’après les formules de calcul des dérivées, P est dérivable partout, et :

P’(x)=a₁+2a₂x+...+ka_kx^k-1+...+na_nx^n-1.

De même si f est une « fraction rationnelle », c’est-à-dire une fonction du type :

x aP(x)/Q(x)

avec P, Q, polynômes, on utilise la formule précédente pour calculer P’ et Q’, et on sait que f sera dérivable partout où elle est définie avec :

f’(x)=[P’(x)Q(x)-P(x)Q’(x)]/Q²(x).

Ainsi on obtient pour la fonction g : x a xⁿ avec n négatif, que la formule g’(x)=nx^n-1 est encore vraie.

Exercices :

1) Préciser où les fonctions suivantes sont dérivables, et calculer leur dérivées : f(x)=(x+1/x)²; g(x)=(x²+x+1)/(x²+1) ; h(x)=2x/(1+x²).

2) Calculer, en revenant aux définitions et en calculant la limite du taux d’accroissement, les dérivées des fonctions suivantes, en précisant où elles sont définies et continues : x³+x²+1 ;  ;  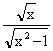; pour n entier naturel non nul ; x(x+1)(x+2)(x+3).

3) Vérifier par le calcul que la dérivée de x^r est rx^r-1, pour tout nombre rationnel r (la fonction est définie sur R₊^*).

4) Soit f une fonction dérivable non nulle sur un intervalle I. On pose L(f)=f’/f, L(f) est donc une fonction définie sur I. Montrer que quelles que soient les fonctions f,g, L(f´g)=L(f)+L(g), L(f/g)=L(f)-L(g), et si f(x)>0 sur I et a entier (ou rationnel) quelconque, L(f^a)=aL(f). Utiliser l’opération L pour calculer facilement la dérivée de (x²+x+1)³/(1-x³)⁵.

5) Soient f,g deux fonctions dérivables en a. On suppose g’(a)¹0 et qu’il existe r>0 tel que pour tout x élément de ]a-r,a+r[-{a} g(x)¹g(a). Montrer que [f(x)-f(a)]/[g(x)-g(a)] tend vers f’(a)/g’(a) quand x tend vers a. Application : calculer les limites, quand x tend vers le nombre a indiqué, des fonctions suivantes : (x³+x-2)/(2x⁴-x-1), a=1 ; [(1+x²)/(1-x²)-1]/[(x²+2)/(x+1)-2], a=0.

6) En utilisant les méthodes du 5) calculer : , avec n,m entiers.

7) La fonction f : R®R, x a|x|, est-elle partout dérivable ? partout continue ? Mêmes questions pour g(x)=x|x|, puis h(x)=D(x)(1-D(x)) où D(x)=x-[x] est la partie décimale de x.

8) Montrer que si f est paire, f’ est impaire, et si f est impaire, f’ est paire. Montrer aussi qu’on peut avoir f’ paire mais f non impaire (prendre f(x)=x+1).

9) Soit f périodique de période T, montrer que f’ est périodique. Montrer qu’on peut avoir f’ périodique et f non périodique (penser à des dérivées constantes).

Tangentes aux courbes

10) Montrer que le demi-cercle de rayon a>0 et de centre O(0,0) est le graphe d'une fonction définie sur [-a,a] : x af(x). Donner l'équation de la tangente en un point (x₀,f(x₀)) au cercle et retrouver que c'est la droite perpendiculaire au rayon passant par le point de contact.

11) On se donne des réels a>b>0. Dans le repère (Oxy) on appelle ellipse E de grand axe a et de petit axe b l'ensemble des points M(x,y) tels que . Que deviendrait cette figure si on avait a=b ? Montrer que E est l'ensemble des point M tels que MF+MF'=2a où F et F' sont les points de coordonnées (c,0) et (-c,0) avec c=. Montrer que les points de E d'ordonnées positives sont le graphe d'une fonction définie sur [-a,a], et que la tangente à E en un point M, qui est par définition la tangente à ce graphe, est une bissectrice des angles déterminés par les droites (MF) et (MF').

12) Soit k>0. On note P la parabole d'équation y=kx². Montrer qu'il existe un réel a>0 tel que, si A est le point (0,a), et D la droite d'équation y= -a, alors un point M est sur P si et seulement si AM=d(M,D) (la distance de M à la droite D)=MH, où H est le projeté orthogonal de M sur D. Que dire de la tangente en un point M de P par rapport au triangle AMH ?

Exercices plus difficiles

13) Soit f une fonction définie sur un intervalle à droite [0,a] avec a>0, continue à droite en 0, et C>1 un réel. Montrer que le quotient a une limite L quand x tend vers 0⁺ si et seulement si f est dérivable à droite en 0. Quel rapport y a-t-il entre L et f'_d(0) ?

14) Soit f une fonction définie sur un intervalle ]x₀-r,x₀+r[. On dit que f admet une dérivée symétrique en x₀ si la limite est un réel l. Ce nombre est nommé la dérivée symétrique en x₀ de f, f'_s(x₀).

a) Montrer que si f a une dérivée à droite et à gauche en x₀, f admet une dérivée symétrique en x₀, et calculer f'_s(x₀) en fonction de f'_d(x₀) et f'_g(x₀).

b) Donner des exemples de fonctions admettant une dérivée symétrique mais pas de dérivée à gauche ni à droite. Etudier la dérivée symétrique de x a|x| en x₀=0.

c) Montrer que si une fonction f admet une dérivée symétrique en un point x₀, et une dérivé à gauche, elle admet aussi une dérivée à droite.

d) Si f admet une dérivée symétrique en x₀, f est-elle forcément continue en x0 ? a-t-elle une limite en x₀ ?

e) Prouver que si f, g ont une dérivée symétrique en x₀, f+g en admet une, et que si f, g sont en plus continues en x₀, (fg) admet une dérivée symétrique en x₀. Dans ces deux cas, calculer (f+g)'_s(x₀) et (fg)'_s(x₀) dans ces deux cas.

2) Accroissements finis

L’application la plus fameuse de la notion de dérivée est l’étude du sens de variation d’une fonction à partir du signe de la dérivée. En fait cette possibilité résulte d’un certain nombre de théorèmes liant le comportement de la dérivée et celui de la fonction. Les plus faciles sont ceux qui partent d’hypothèses sur la fonction et qui en déduisent des propriétés de la dérivée.

Propriété 1 : Si f est dérivable en a et qu’il existe un intervalle ]a-r,a] avec r>0, sur lequel f(x)£f(a), alors f’(a)³0 (fig 1). Si on a f(x)³f(a) sur un tel intervalle, alors f’(a)£0. De même, si f(x)³f(a) sur un intervalle [a,a+r[, alors f’(a)³0 et si f(x)£f(a) sur un tel intervalle, alors f’(a)£0.

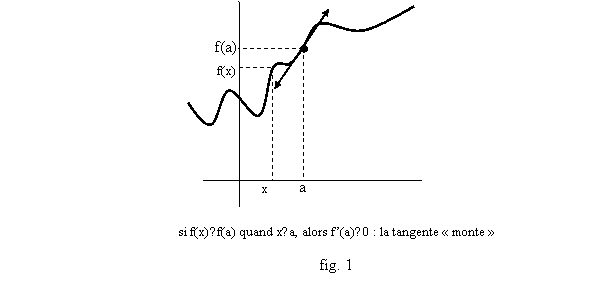
Démonstration : on fait le premier cas, les autres se traitent de la même façon. On a supposé que sur ]a-r,a], f(x)£f(a). Alors f(x)-f(a)£0 et si x<a, comme x-a<0, cela donne [f(x)-f(a)]/(x-a)³0. Comme la limite d’une fonction positive est positive, on a forcément f’(a)³0.

On peut tirer de ce résultat des conséquences importantes sur les valeurs de la dérivée, si la fonction est monotone, ou si elle a un maximum ou un minimum. Précisons la définition suivante :

Définition : soit f définie sur un intervalle I et a un élément de I. On dit que f présente un maximum en a si f(x)≤f(a) pour tout x élément de I. On dit que f présente un maximum strict en a si f(x)<f(a) pour tout x de I différent de a. On définit de même un minimum, un minimum strict. Si f présente un maximum ou un minimum, on dit qu’elle présente un extremum en a, et si c’est un maximum ou un minimum strict, on parle d’extremum strict. Enfin on dit que f présente un maximum local en a si on peut isoler un intervalle autour de a, entièrement inclus dans I, qui peut s’écrire par exemple ]a-r,a+r[ avec un réel r>0, telle que f(x)≤f(a) si x est entre a-r et a+r. On définit de même un maximum local strict, minimum local, minimum local strict, extremum local, extremum local strict.

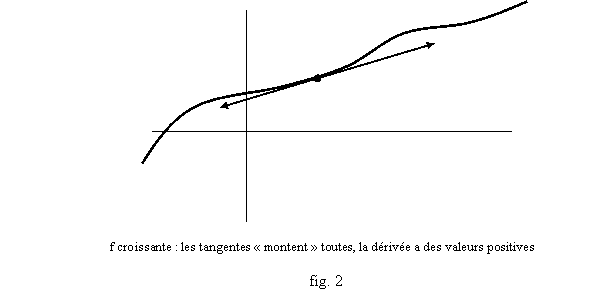
Théorème 2 :

a. Si f est croissante et dérivable sur I, alors f’(x)³0 sur I (fig 2).

b. Si f est décroissante et dérivable sur I, f’(x)£0.

c. Soit f définie sur un intervalle I ; si a est intérieur à I, c’est-à-dire qu’il y a r>0 tel que ]a-r,a+r[ÍI, et si f est dérivable en a et a un extremum en a, alors f’(a)=0 (fig 3).

Démonstration : ce sont des applications de la propriété 1. Par exemple si f est croissante on aura pour tout a et tout x, si x<a alors f(x)£f(a) et si x>a alors f(x)³f(a), donc on aura bien f’(a)³0. On a la même chose pour f décroissante. Si f a un extremum en a, par exemple un minimum local, alors il y a un r’>0 tel que f(x)³f(a) sur ]a-r’,a+r’[ÇD_f. Soir R=min(r,r’), alors sur ]a-R,a+R[ f est définie et f(x)³f(a). en particulier f(x)³f(a) si a-R<x<a, ce qui entraîne f’(a)£0, et f(x)³f(a) pour a<x<a+R, donc f’(a)³0. Finalement f’(a)=0.

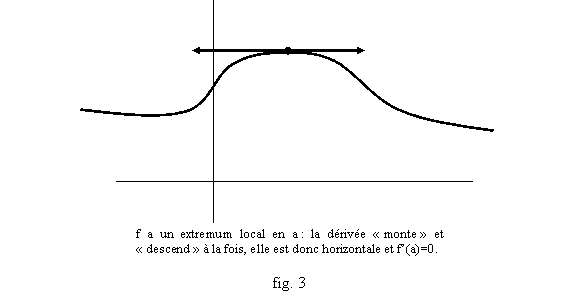
Le principal intérêt du théorème précédent est une méthode de recherche des extrema : si f est dérivable sur un intervalle I, pour rechercher les extrema locaux de f sur I, on peut calculer f’ et résoudre l’équation f’(x)=0. Toutes les solutions ne sont pas des extrema, mais s’il y a des extrema intérieurs à I, ils sont parmi les points trouvés. Il faut après étudier chacun de ces points pour vérifier si c’est un extremum, et étudier aussi les bornes de I, car elles peuvent être des extrema sans que la dérivée y soit nulle.

Remarque : La notion d’extremum local correspond à un extremum atteint à l’intérieur d’un intervalle. Si f atteint son maximum aux bornes de l’intervalle, il n’y a aucune raison qu’on y ait une dérivée nulle (un exemple : sur la fig. 5, la fonction est maximum en b mais ce n’est pas un « extremum local », et on n’a pas de dérivée nulle).

En plus du théorème précédent, ce dont on a besoin c’est d’un résultat du type : « si f’ est positive, f est croissante ». Pour obtenir les théorèmes souhaités, il faut adopter la démarche inverse de la propriété 1 et du théorème 2 : on est parti d’hypothèses sur les valeurs de f et en fait des taux d’accroissements [f(x)-f(a)]/(x-a), on en a déduit des précisions sur f’. Il faut maintenant montrer que ces taux d’accroissements eux-mêmes ont des valeurs qu’on peut connaître si on connaît les valeurs de f ’.

Le premier de ces théorèmes est le théorème de Rolle : il dit que si aux deux bornes d’un intervalle f prend la même valeur, alors il y a forcément un point où la dérivée s’annule entre les deux. Autrement dit, une fonction dont la dérivée ne s’annule pas sur un intervalle ne peut pas avoir un accroissement nul entre les bornes.

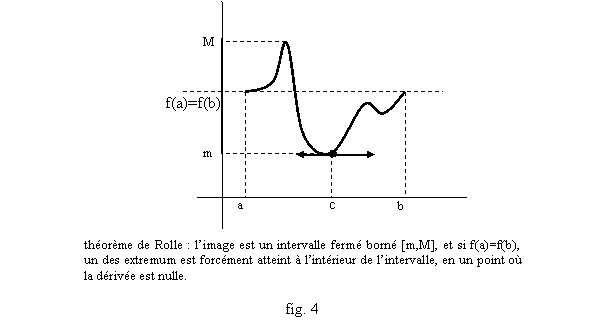
Théorème 3 (théorème de Rolle) : Si f est une fonction continue sur un intervalle [a,b] (a<b), dérivable sur ]a,b[, et si f(a)=f(b), alors il y a un point c dans l’intervalle ]a,b[ tel que f’(c)=0.

Démonstration : f étant continue a un minimum et un maximum sur [a,b], on note m et M les valeurs minimales et maximales de f. Soit m=M dans ce cas f est constante sur [a,b], soit m<M, dans ce cas l’un des deux nombres m, M est différent de f(a)=f(b). Il y a donc un point c strictement intérieur à ]a,b[ où f atteint cette valeur, minimale ou maximale, de toute façon f a un extremum en c. Comme c est intérieur à ]a,b[, on peut appliquer le théorème 2 : f’(c)=0 (fig 4).

On peut généraliser ce résultat, mais au lieu de trouver un point c où f’(c)=0, on trouve un point c où f’(c) est égal à l’accroissement moyen de f entre a et b, c’est-à-dire le taux T=[f(b)-f(a)]/(b-a) : on compare pour cela de manière assez naturelle f avec la fonction

x af(a)+(x-a)T.

Cela donne le théorème des accroissements finis. On a une interprétation géométrique usuelle : si A, B et C sont les points du graphe de f de coordonnées (a,f(a)), (b,f(b)) et (c,f(c)), le taux d’accroissement T est le coefficient directeur (la « pente ») de la droite (AB), et f’(c) est la pente de la tangente en C à la courbe ; dire que T=f’(c) revient à dire que ces deux droites ont même pente, c’est-à-dire qu’elle sont parallèles (révisions utiles : équations de droites, graphes des fonctions affines, etc.).

Théorème 4 (théorème des accroissements finis) : Si f est une fonction continue sur [a,b] (a<b) et dérivable sur ]a,b[, il y a c dans ]a,b[ tel que : f’(c)=[f(b)-f(a)]/(b-a) (fig 5).

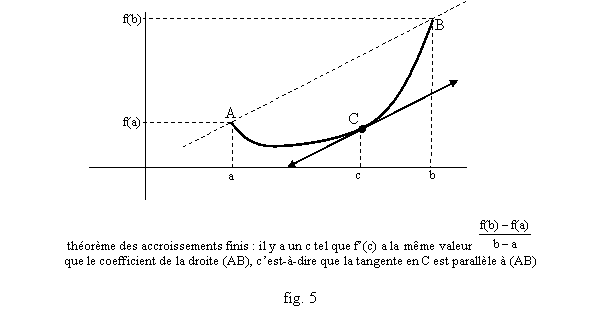
Démonstration : on part de f et on pose g(x)=f(x)-T(x-a) où T=[f(b)-f(a)]/(b-a) est le taux d’accroissement. Alors g est continue sur [a,b], dérivable sur ]a,b[, et g’(x)=f’(x)-T car la dérivée de x aT(x-a) est la constante T. De plus

g(a)=f(a)-T(a-a)=f(a)

et

g(b)=f(b)-T(b-a)=f(b)-(b-a)[f(b)-f(a)]/(b-a)=f(b)-(f(b)-f(a))=f(a).

Donc on peut appliquer le théorème de Rolle à g, il y a c dans ]a,b[ tel que g’(c)=0 c’est-à-dire f’(c)=T.

On remarquera que dans ces deux théorèmes il n’est pas supposé que f est dérivable en a et b. Ils s’appliquent même s’il y a une tangente verticale en ces points ou pas du tout de tangente.

Le théorème des accroissements finis a une foule d’applications.

Théorème 5 (« inégalité des accroissements finis ») : si f est une fonction dérivable sur ]a,b[, continue sur [a,b], et s’il y a un réel m tel que, pour tout x de ]a,b[, f’(x)³m, alors [f(b)-f(a)]/(b-a)³m. Et si on a pour tout x de ]a,b[, f’(x)>m, alors [f(b)-f(a)]/(b-a)>m. De même s’il y a M tel que pour tout x de ]a,b[, f’(x)£M (respectivement f’(x)<M), alors [f(b)-f(a)]/(b-a)£M (respectivement [f(b)-f(a)]/(b-a)<M).

Enfin si |f’(x)|£M (resp. <M) pour tout x, on aura pour tous c,d dans l’intervalle, l’inégalité : |f(d)-f(c)|£M|d-c| (resp. |f(d)-f(c)|<M|d-c|).

Démonstration : on applique le théorème des accroissements finis à f sur [a,b] : comme [f(b)-f(a)]/(b-a) est égal à une valeur f’(c) de la dérivée, toute inégalité sur la dérivée rejaillit sur ce nombre. L’inégalité avec les valeurs absolues s’obtient en remarquant qu’on a |u|£M si et seulement si : -M£u£M. On se ramène donc a une inégalité du premier type étudié.

Théorème 6 : Soit f une fonction définie sur un intervalle I, continue sur I et dérivable à l’intérieur de I.

a. Si f’(x)³0 sur l’intérieur de I, f est croissante, et si f’(x)>0 sur l’intérieur de I, f est strictement croissante.

b. Si f’(x)£0 (respectivement f’(x)<0) sur l’intérieur de I, f est décroissante (respectivement strictement décroissante).

c. S’il y a un point a intérieur à I où f’ change de signe, c’est-à-dire que f’ est d’un signe sur ]a-r,a[ et du signe opposé sur ]a,a+r[, alors f présente un extremum local en a. Et si le changement de signe est strict, il s’agit d’un extremum strict.

Démonstration :

Ce résultat repose sur l’inégalité des accroissements finis. Par exemple si f’(x)>0 sur l’intérieur de l’intervalle, et si on prend u,v dans I avec u<v, l’inégalité du théorème 6, avec a=u, b=v, m=0, s’applique car l’intérieur ]u,v[ de [u,v] est bien constitué de points intérieurs de I, donc de points x où f’(x)>0. On a donc [f(v)-f(u)]/(v-u)>0 et comme v-u>0, cela donne f(v)-f(u)>0 ou f(v)>f(u). Ainsi : v>u Þ f(v)>f(u), et f est bien strictement croissante.

Les autres propriétés de monotonie se traitent similairement. Quand à la dernière propriété, supposons par exemple que f’(x)<0 sur ]a-r,a[ et f’(x)>0 sur ]a,a+r[. Les raisonnements précédents prouvent que f est strictement décroissante sur ]a-r,a], donc f(u)>f(a) si a-r<u<a, et strictement croissante sur a<u<a+r, donc f(u)>f(a) si a<u<a+r. Finalement f a un minimum local strict en a. Les autres cas possibles (f’ positif avant a, négatif après, etc.) se règlent de même.

Il convient de ne pas confondre les différentes propriétés : on a, en mettant côte à côte les théorèmes 2 et 6, que f est croissante si et seulement si f’(x)³0 sur I, et décroissante si et seulement si f’(x)£0. Par ailleurs d’après le théorème 6, si f’(x)>0, f est strictement croissante, et strictement décroissante si f’(x)<0. Mais on n’a aucun théorème nous donnant le signe strict de la dérivée si f est strictement monotone. Ainsi f(x)=x³, elle est strictement croissante sur R et vérifie f’(0)=0 (cf. figures au chapitre 1). Mais on peut faire « pire ».

Pour cela, voyons un contre exemple plus compliqué (attention, partie en italique, à lire uniquement si on veut aller plus loin) :

Soit f(x)= -2x³+3x². C’est un polynôme, de dérivée f’(x)=6(-x²+x)=6x(1-x), strictement positive sur ]0,1[, donc strictement croissante sur [0,1]. Mais on a f_d’(0)=f_g’(1)=0. Notons que f(0)=0, f(1)=1. Maintenant on définit la fonction g suivante : si n³1, sur l’intervalle

I_n=[1/(n+1),1/n],

on pose

g(x)=1/2ⁿ+(1/2ⁿ)f[n(n+1)(x-1/(n+1))].

Cette définition est correcte puisque

g(1/(n+1))=1/2ⁿ+(1/2ⁿ)f(0)=1/2ⁿ,

et

g(1/n)=1/2ⁿ+(1/2ⁿ)f[n(n+1)(1/n-1/(n+1))]=1/2ⁿ+(1/2ⁿ)f(1)=1/2^n-1.

Donc le calcul sur I_n+1 donnera aussi

g(1/(n+1))=1/2^(n+1)-1=1/2ⁿ,

c’est-à-dire que les deux définitions issues de I_n et I_n+1 coïncident au point 1/(n+1). Ainsi g est correctement définie et continue sur ]0,1], et on la prolonge par g(0)=0, ce qui la rend continue puisque g(x)£1/2^n-1 si x£1/n, donc g tend vers 0 en 0.

Sur I_n,

g’(x)=n(n+1)/2ⁿf’[n(n+1)(x-1/(n+1))]

par dérivation de fonctions composées, donc si 1/(n+1)<x<1/n, on aura :

0<n(n+1)(x-1/(n+1))<1

et donc

g’(x)>0.

Ceci prouve que g est dérivable sur l’intérieur des I_n, et strictement croissante dessus, donc strictement croissante sur [0,1] puisque si x<y, ou bien ils sont dans le même I_n et g étant strictement croissante sur I_n, g(x)<g(y), ou bien il y a n tel que x<1/n<y, mais alors x est dans I_p et y est dans I_q pour un p>q, donc par construction g(x)£1/2^p-1£1/2^q£g(y), et l’une au moins de ces inégalités est stricte (sinon x et y seraient dans le même I_p=I_q). On a donc encore g(x)<g(y). Enfin si x=0, par construction comme y est dans un I_n, g(y)>g(x)=0.

Ainsi on a une fonction strictement croissante, mais toujours par dérivation de fonctions composées, dans I_n,

g_d’(1/(n+1))=n(n+1)/2ⁿf_d’[n(n+1)(1/(n+1)-1/(n+1))]=n(n+1)/2ⁿf_d’(0)=0.

Et dans I_n+1,

g_g’(1/(n+1))=(n+1)(n+2)/2ⁿ⁺¹f_g’[(n+1)(n+2)(1/(n+1)-1/(n+2))]=(n+1)(n+2)/2ⁿ⁺¹f_g’(1)=0.

Donc cela signifie que [g(x)-g(1/(n+1))]/(x-1/(n+1)) a la même limite nulle à droite et à gauche, donc a pour limite 0, et g est finalement dérivable en tous les points 1/(n+1), avec g’(1/(n+1))=0.

Enfin si 1/(n+1)<x£1/n, on a 1/x<n+1 et g(x)£1/2^n-1, il s’ensuit que g(x)/x<(n+1)/2^n-1 avec n=n(x) tel que n£1/x<n+1, c’est-à-dire que n=E(1/x). D’où :

g(x)/x<(E(1/x)+1)/2^E(1/x)-1.

Quand x tend vers 0, en restant positif, E(1/x) tend vers +¥, et (E(1/x)+1)/2^E(1/x)-1 tend donc vers 0 d’après les limites de références données à la fin de ce chapitre (cf. paragraphe 3 pour les fonctions exponentielles). Ceci prouve que g(x)/x=(g(x)-g(0))/(x-0) tend vers 0 quand x tend vers 0, donc g’_d(0)=0. On peut conclure (fig 6 - un dessin est utile : on a empilé des « marches d’escalier », de plus en plus étroites et petites, semblables à f) :

g est une fonction strictement croissante et continue bijective de [0,1] sur lui-même, mais de dérivée nulle en 0 et en 1, 1/2, 1/3, 1/4,etc. bref en une infinité de points.

On voit qu’on peut avoir des cas « pathologiques » de fonctions strictement monotones mais dont la dérivée s’annule en beaucoup d’endroits. On peut même construire des fonctions strictement croissantes sur [0,1] mais dérivable nulle part, ou alors dérivable en beaucoup de points mais de dérivée nulle partout où elle est définie, etc. Néanmoins la plupart des fonctions rencontrées naturellement sont plus régulières que cela, et on les étudie en général en étudiant le signe de leur dérivées, et en découpant D_f en intervalle où f’ est de signe strictement constant, et où la fonction est strictement monotone.

Pour conclure, signalons qu’une fonction ne peut pas avoir sa dérivée « trop nulle » et être strictement monotone ; en fait :

Théorème 7 : Une fonction continue est constante sur un intervalle I si et seulement si elle est dérivable, de dérivée nulle, en tout point intérieur à I.

Démonstration : si f est constante on a déjà prouvé que f’(x)=0 en tout point de I, et si f’(x)=0 en tout point intérieur à I, le théorème 6 prouve que, comme f’(x)³0 et f’(x)£0, f est à la fois croissante et décroissante sur I, donc constante.

Théorème 8 : Soient f,g deux fonctions continues sur un intervalle I et dérivables sur l’intérieur de I, alors f’=g’ sur l’intérieur de I si et seulement si f-g est une fonction constante.

Démonstration : on applique le théorème 7 à h=f-g, en remarquant que h’=(f-g)’=f’-g’ est nul si et seulement si f’=g’.

Une autre conséquence de tout cela est l’obtention de majorations entre plusieurs fonctions.

Propriété 9 : Soient f et g des fonctions continues sur un intervalle [a,b] avec a<b, dérivables sur ]a,b[, telles que f’(x)£g’(x) (respectivement f’(x)<g’(x)) sur I. Alors on a : f(b)-f(a)£g(b)-g(a) (resp. f(b)-f(a)<g(b)-g(a)).

Démonstration : On pose h(x)=g(x)-f(x). Alors pour tout x dans I, on a : h’(x)=g’(x)-f’(x)≥0, d’après l’hypothèse (resp. h’(x)>0). Donc h est une fonction croissante (resp. strictement croissante), et on peut écrire :

h(b) ≥h(a) (resp. h(b)>h(a)),

c’est-à-dire : g(b)-f(b) ≥g(a)-f(a) (resp. g(b)-f(b)>g(a)-f(a))

et finalement : f(b)-f(a)£g(b)-g(a) (resp. f(b)-f(a)<g(b)-g(a)).

Exercices :

1) Soit P(x)=x²+ax+b. Montrer que pour toute paire (x₁,x₂) tel que x₁<x₂ il y a c tel que x₁<c<x₂ et P(x₁)-P(x₂)=(2c+a)(x₁-x₂). Calculer c en fonction de x₁ et x₂.

2) Soit a,b deux réels. Montrer qu’il y a c tel que a³-b³=3c²(a-b). En déduire que a²+ab+b² est strictement positif sauf si a=b=0.

3) Soit f une fonction continue sur un intervalle [a,b] tel que 0<a<b, dérivable sur ]a,b[, et telle que f(a)=f(b)=0. Montrer qu’il y a une tangente à la courbe qui passe par l’origine (on pourra montrer que la tangente en c passe par l’origine si et seulement si f(c)-cf’(c)=0 puis chercher un nombre c vérifiant cette égalité).

4) Etudier les variations des fonctions f suivantes sur R, et en déduire le nombre de solutions de l’équation f(x)=0 : f(x)=x³, f(x)=x³-x, f(x)=x⁴-2x²-1.

5) Soit des réels fixés a₁<a₂<…<a_n, on pose P(x)=(x-a₁)…(x-a_n).

a. Montrer que si x n’est pas un des a_i, P’(x)/P(x)=1/(x-a₁)+1/(x-a₂)+…+1/(x-a_n).

b. Montrer que P’ admet, pour tout i, une racine c telle que a_i<c<a_i+1.

c. Retrouver ce résultat en étudiant la fonction F(x)=1/(x-a₁)+1/(x-a₂)+…+1/(x-a_n).

6) (Rolle généralisé) Soit f une fonction continue sur un intervalle [a,+¥[, dérivable sur ]a,+¥[, et telle que . On veut montrer qu’il y a c>a tel que f’(c)=0.

a. Si f est constante, montrer que c existe.

b. Si f est non constante, justifier qu’on peut prendre x₀>a tel que f(x₀)¹f(a).

c. Si f(x₀)>f(a), montrer qu’il y a un intervalle ]A,+¥[ avec A>a, où f(x)<f(x₀). En déduire que f admet un maximum sur [a,+¥[, et expliquer comment on trouve le point c.

d. Si f(x₀)<f(a), montrer qu’on peut changer la preuve précédente pour obtenir aussi c.

7) Soit f une fonction dérivable sur R, telle que . Montrer qu’il existe c dans R tel que f’(c)=0 (adapter les raisonnements de l’exercice précédent).

Exercices plus difficiles

8) Soit f une fonction définie et continue sur [0,1], dérivable sur ]0,1[, et telle que f(0)=0, f(1)=1. Montrer que pour tout entier n, on peut trouver une suite croissante c₁<c₂<…<c_n dans ]0,1[ telle que : . Montrer qu'on peut prendre, pour tout k, . Montrer qu'on peut aussi trouver une suite 0<a₁<a₂<…<a_n<1 vérifiant .

9) Soit f une fonction définie sur un intervalle [a,b], dérivable, et telle que f’(a)<0 et f’(b)>0.

a. Montrer qu’il y a un intervalle ]a,a+r[ sur lequel f(x)<f(a), et un intervalle ]b-r’,b[ où f(x)<f(b).

b. En déduire qu’il y a c dans ]a,b[ tel que f’(c)=0.

10) (Théorème de Darboux des valeurs intermédiaires pour les dérivées) On veut prouver qu’une fonction dérivée satisfait la conclusion du théorème des valeurs intermédiaires.

Soit f une fonction dérivable sur [a,b], et m un nombre qui est entre f’(a) et f’(b), par exemple f’(a)<m<f’(b). Montrer qu’il existe c dans ]a,b[ tel que f’(c)=m (appliquer l’exercice précédent à la fonction x af(x)-mx).

11) Soit f une fonction dérivable sur ]a,b[, continue sur [a,b[, telle que . Montrer que si l=±¥, alors la courbe de f admet une tangente verticale au point (a,f(a)), et si l est un nombre (fini), alors f est dérivable en a et f’(a)=l (on cherchera une fonction a telle que pour tout x, [f(x)-f(a)]/(x-a)=f’(a(x)) et que ).

12) Soit f, g des fonctions continues sur I, dérivables sur I\{x₀}, telles que f(x₀)=g(x₀)=0. Montrer que si alors .

13) Soient f, g deux fonctions définies sur [a,b], avec g(a)¹g(b) et f(a)¹f(b) ; montrer qu’il y a un point c dans ]a,b[ tel que g’(c)¹0 et .

14) Soit f une fonction continue dans un intervalle [a,b]. On suppose que f '_d(x) existe en tout point x de [a,b].

a) Montrer que si f'_d(c)<0 et f'_d(d)>0, il existe deux points distincts de ]c,d[ où f prend la même valeur.

b) Montrer que si les bornes de f'_d sur ]a,b[ sont m et M sur ]a,b[ (avec m réel, ou égal à -¥, M réel, ou égal à +¥), alors l'ensemble des nombres avec a<x<y<b est égal à ]m,M[ sauf si f est affine auquel cas cet ensemble est {m}.

c) Montrer que si f '_g(x) existe en tout point de ]a,b[, les bornes supérieures et inférieures de f '_g et de f '_d sont égales dans ]a,b[.

d) On suppose f dérivable dans un intervalle ouvert I contenant [a,b], on pose g=f ', et on suppose g dérivable sur ]a,b[ mais pas nécessairement continue en a ou b. Montrer qu'on peut trouver c dans ]a,b[ tel que : .

3) Fonctions élémentaires.

On rappelle dans ce paragraphe quelques fonctions d’usage courant, la plupart déjà étudiées au lycée.

Fonctions trigonométriques

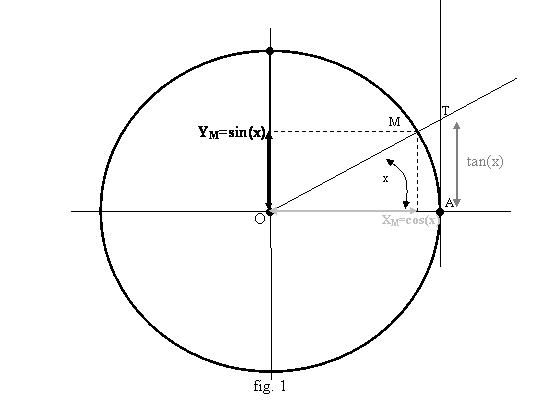
Sur le cercle trigonométrique (centre : l’origine du repère orthonormé, rayon : 1), on peut repérer un point M par ses coordonnées (X_M,Y_M), qui sont telles que X_M²+Y_M²=1 si et seulement si le point est sur le cercle (cela signifie que le carré de la distance OM vaut 1). On peut aussi repérer le point M par l’angle x entre le segment [OM] et l’horizontale (OA). On fait correspondre les deux en posant : cos(x)=X_M, sin(y)=Y_M. Si on prolonge la droite (OM), elle coupe la tangente (verticale) au cercle menée de A en un point T, et on a alors AT=sin(x)/cos(x) (en fait ce rapport peut être négatif, mais si on oriente la droite (AT) « vers le haut », les distances devenant des mesures algébriques, positives quand elles vont vers le haut, négatives vers le bas, cette mesure vaudra alors toujours sin(x)/cos(x)). Ce nombre est par définition la tangente de x, tan(x). Il est défini quand la droite (OM) n’est pas parallèle à (AT), c’est-à-dire quand x n’est pas l’angle droit (±p/2). Tout ceci est rappelé sur la figure 1. Les angles étant usuellement mesurés en radian, on peut prendre pour x la longueur (mesurée en suivant le cercle) de l’arc AM; la longueur du cercle est alors de 2p, les fonctions définies ci-dessus sont toutes périodiques de période 2p. Par ailleurs comme OM=1, donc OM²=1, grâce au théorème de Pythagore, on obtient la fameuse relation :

cos²(x)+sin²(x)=1

De nouveau, on va admettre les faits de base sur ces fonctions, qui nous entraîneraient trop loin en géométrie (et pas seulement) si on essayait de les démontrer.

D’abord, on donne les « formules d’addition », dont on peut déduire de nombreuses autres formules semblables :

cos(x+x’)=cos(x)cos(x’)-sin(x)sin(x’)

sin(x+x’)=cos(x)sin(x’)+sin(x)cos(x’)

Ces formules sont simples à vérifier, mais comme elles reposent sur du calcul vectoriel, et qu’on veut limiter la géométrie ici, nous ne les démontrerons pas.

Angles associés

Prenons un point M du cercle correspondant à l’angle x. Alors les « angles associés » à x : -x, x+p, p-x, p/2-x, correspondent à des points qui se déduisent de M par des symétries respectivement par rapport à l’axe des x, au centre O du repère, à l’axe des y, à la droite d’équation Y=X. Au niveau des coordonnées, cela se traduit respectivement par : changer (X,Y) en (X,–Y), changer (X,Y) en (-X,-Y), changer (X,Y) en (-X,Y), changer (X,Y) en (Y,X). Tout ceci est représenté fig. 2.

La conséquence de tout ceci, c’est les formules :

cos(-x)=cos(x), sin(-x)= -sin(x), d’où tan(-x)= -tan(x) (cosinus est paire, sinus et tangente sont impaires) ;

cos(x+p)= -cos(x), sin(x+p)=-sin(x), d’où tan(x+p)=tan(x).

cos(p-x)= -cos(x), sin(p-x)=sin(x), d’où tan(p-x)=-tan(x) ;

cos(p/2-x)=sin(x), sin(p/2-x)=cos(x), tan(p/2-x)=1/tan(x).

Une inégalité

Maintenant reprenons le dessin de la fig. 1. On a une inégalité qui va nous donner toutes les limites importantes concernant les fonctions trigonométriques :

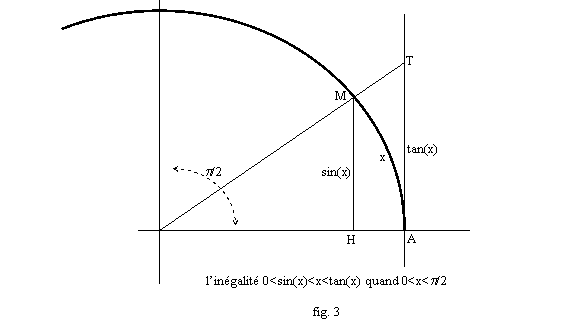
Pour tout x tel que, 0<x</2, on a : 0<sin(x)<x<tan(x).

Explication : sur le dessin (cf. fig. 3), cela s’écrit HM<arc AM<AT, ce qui est assez intuitif.

1ère Conséquence : sinus, cosinus et tangente sont des fonctions continues.

En effet l’inégalité 0<sin(x)<x et le théorème des gendarmes prouve que, quand x tend vers 0 en restant positif, sin(x) tend vers 0. Comme sin(-x)= -sin(x), 0 est la limite quand x tend vers 0 mais en restant négatif. Finalement on a . Comme cos²(x)+sin²(x)=1 pour tout x, et que cos(x)>0 quand x est entre -p/2 et p/2, on en déduit , et, par composition des limites, cos(x) tend vers quand x tend vers 0. Dans ce cas, en utilisant les formules d’addition, on trouve, si a et x sont deux réels :

cos(x)=cos[(x-a)+a]=cos(x-a)cos(a)-sin(x-a)sin(a)

sin(x)=sin[(x-a)+a]=cos(x-a)sin(a)+sin(x-a)cos(a)

quand x tend vers a, x-a tend vers 0, et par les règles de composition et d’opérations sur les limites :

cos(x) tend vers cos(0)cos(a)-sin(0)sin(a)=1´cos(a)-0´sin(a)=cos(a)

sin(x) tend vers cos(0)sin(a)+sin(0)cos(a)=1´sin(a)+0´cos(a)=sin(a)

ce qui prouve que les fonctions sinus et cosinus sont continues. Par opérations sur les fonctions, la fonction tangente, quotient des précédentes, est continue là où elle est définie.

2^ère Conséquence : sinus, cosinus et tangente sont des fonctions dérivables en tout point,

et on a pour tout x les relations :

sin’(x)=cos(x)

cos’(x)= -sin(x)

tan’(x)=1+tan²(x)=1/cos2(x)

si x>0, on a d’après la même inégalité :

0<sin(x)<x<tan(x) Þ 0<1<x/sin(x)<1/cos(x), en divisant tout par sin(x)>0.

Comme cos(x) tend vers 1 si x tend vers 0, le théorème des gendarmes prouve que x/sin(x) tend vers 1 quand x tend vers 0 en restant positif. Comme la limite est la même quand x est négatif (puisque sin(-x)= -sin(x)), on obtient et, en prenant l’inverse :

cette limite est à connaître par cœur. Elle nous permet d’obtenir la dérivée en 0 de sinus, puisque . On a donc sin’(0)=1.

Par ailleurs les formules d’additions donnent pour tout x :

cos(x)=cos(x/2+x/2)

=cos(x/2)cos(x/2)-sin(x/2)sin(x/2)

=cos²(x/2)-sin²(x/2)

=[1-sin²(x/2)]-sin²(x/2)

=1-2sin²(x/2).

Ce qui donne comme taux d’accroissement :

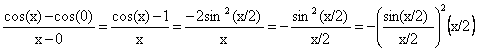
quand x tend vers 0, le quotient entre parenthèses tend vers 1 (toujours la même ) limite et x/2 vers 0, donc le taux d’accroissement tend vers 0.

Maintenant soit a un réel quelconque et x¹a. On a déjà calculé :

cos(x)=cos[(x-a)+a]=cos(x-a)cos(a)-sin(x-a)sin(a)

sin(x)=sin[(x-a)+a]=cos(x-a)sin(a)+sin(x-a)cos(a)

On en tire :

et

quand x tend vers a, x-a tend vers 0 et on a :

et

Grâce au règles d’opérations sur les limites, on en déduit que le premier taux tend vers :

0´cos(a)-1´sin(a)=-sin(a)

et le deuxième vers :

0´sin(a)+1´cos(a)=cos(a).

On a montré ce qu’on voulait, que la dérivée de cos en a est –sin(a), et celle de sinus cos(a).

Par ailleurs la formule de dérivée d’un quotient donne que tan est dérivables en tout point où elle est définie avec :

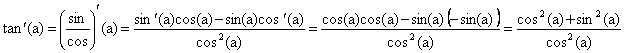si on sépare le quotient en une somme, on trouve :

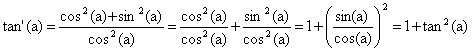
tandis que si on remarque que cos²(a)+sin²(a)=1 on obtient :

.

3^ème conséquence : étude des variations des fonctions trigonométriques.

Des valeurs de ces dérivées on tire les sens de variation des fonctions. Par exemple comme sin(x)>0 sur ]0,p[, et que cos’(x)= -sin(x), cos est strictement décroissante sur [0,p]. Comme elle est paire (cos(-x)=cos(x)), elle est croissante sur [-p,0], et comme elle est périodique de période 2p, son tableau de variation se répète.

De même comme cos(x)>0 sur ]0,p/2[, et cos(x)<0 sur ]p/2,p[, et comme sin’(x)=cos(x), on en tire que sinus est strictement croissante sur [0,p/2], strictement décroissante sur [p/2,p], et aussi décroissante sur [-p,-p/2], croissante sur [-p/2,0], par symétrie car sinus est impaire. La remarque sur la périodicité vaut encore. On tire de tout cela l’allure des courbes (fig. 4).

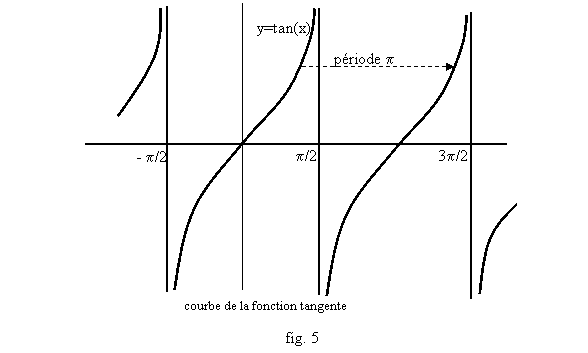
La relation : tan’(x)=1+tan²(x) prouve que tan’(x) est toujours strictement positive, la fonction tangente est donc strictement croissante sur tout intervalle où elle est définie. Par ailleurs elle est définie si cos(x)≠0, donc en tout x distinct de -5p/2, -3p/2, -p/2, p/2, 3p/2, 5p/2, 7p/2, ... Elle est périodique de période p. Regardons sur l’intervalle ]- p/2, p/2[ ; quand x tend vers p/2 (en restant <p/2), cos(x) tend vers 0 en restant positif, et sin(x) tend vers 1. donc tan(x) tend vers +∞, et comme tan est impaire, elle tend vers -∞ quand x tend vers -p/2 en restant >-p/2. On a représenté cela fig. 5.

Fonctions exponentielles et logarithmes.

La fonction logarithme népérien est une fonction, notée ln, ou parfois Log, est une fonction définie sur R₊^* dont la dérivée est 1/a en tout point a>0, et qui vaut 1 quand x=0.

On admet qu’une telle fonction existe (les démonstrations sont bien au-delà du programme…). D’après ce qu’on a vu, cette fonction est unique si sa dérivée est fixée et qu’on a fixé ln(1)=0. Les autres fonctions dont la dérivée est 1/x sont les fonctions sommes du logarithme et d’une constante (et pour avoir ln(1)=0 seule la constante 0 convient d’où l’unicité).

Comme ln’(a)=1/a>0 sur R₊^*, la fonction ln est strictement croissante. Son intérêt provient d’une formule fondamentale :

Pour tous réels strictement positifs a et b, on a : ln(ab)=ln(a)+ln(b).

Pour la démontrer, fixons le réel a>0. Il suffit de prouver que les deux fonctions x a ln(ax) et x a ln(a)+ln(x) sont égales. Etudions donc leur différence f(x)=ln(ax)-ln(x)-ln(a). Cette fonction est définie sur R₊^*, et dérivable d’après les théorèmes de compositions et de calculs sur les dérivées, f est dérivable et sa dérivée vaut :

f ’(x)=[ln(ax)]’-[ln(a)]’-[ln(x)]’ (dérivée d’une somme)

f ’(x)=(ax)’[1/(ax)]-0-1/x (dérivée de la composition de x a ax et de ln)

f ’(x)=a/(ax)-1/x

f ’(x)=1/x-1/x=0

Donc la fonction f est constante. Comme f(1)=ln(a´1)-ln(1)-ln(a)=ln(a)-ln(a)=0, cette constante est 0 et on a prouvé que ln(ax)-ln(a)-ln(x)=0 pour tout réel x>0, ce qu’on voulait.

On en déduit les formules usuelles :

Si x>0, on a :

ln(x²)=ln(x´x)=ln(x)+ln(x)=2ln(x),

ln(x³)=ln(x²´x)=ln(x²)+ln(x)=2ln(x)+ln(x)=3ln(x), etc.

Bref pour tout réel x>0 et tout entier naturel n, on aura ln(xⁿ)=n.ln(x).

Par ailleurs si a,b>0, posons q=a/b. Alors q´b=(a/b)b=a, donc ln(qb)=ln(a) et ln(q)+ln(b)=ln(a), d’où finalement ln(q)=ln(a)-ln(b). C’est une nouvelle formule :

Si a,b>0, on a ln(a/b)=ln(a)-ln(b).

On peut citer un cas particulier important, en prenant a=1 :

Si b>0, ln(1/b)= -ln(b).

Un peu comme pour la formule du quotient, si x>0 est fixé, posons , on a alors a²=x, donc ln(a²)=ln(x) et 2ln(a)=ln(x) ce qui donne :

Si x>0, .

On peut aussi généraliser cette formule, on a si x>0, et n≥1 est un entier :

.

Remarquons que le fait que la dérivée de ln(x) soit 1/x signifie qu’on a des limites de référence, admises a priori mais qu’on pourra utiliser :

.

On a d’autres limites fondamentales à connaître.

Premièrement ln(x) dépasse n’importe quel nombre fixé d’avance, si x est assez grand : en effet, d’après les relations précédentes on a ln(2ⁿ)=n´ln(2), avec ln(2)>ln(1)=0. Si on prend un réel M même grand, il suffit de prendre un entier n>M/ln(2) pour avoir n´ln(2)>M et donc ln(2n)>M. Comme ln est croissante, on aura même ln(x)>M pour tous les x plus grand que 2n. Cette observation signifie que ln tend vers +∞ en +∞ (c’en est même la vraie définition).

.

Comme ln(1/x)= -ln(x), on en déduit que ln tend vers –∞ quand x tend vers 0⁺.

.

Appliquons maintenant l’inégalité des accroissements finis : comme 1/t=ln’(t)<1 si t>1, on aura pour tout nombre x>1, en appliquant l’inégalité sur [1,x] :

ln(x)-ln(1)<1´(x-1) donc : ln(x)<x-1.

Conséquence : si x>1, ln(x)<x (puisque x-1<x).

(On peut aussi poser f(x)=x-ln(x). f est définie si x>0, et dérivable avec f ’(x)=1-1/x. Cette dérivée est strictement positive si x>1, car alors 1/x<0. Ainsi f est strictement croissante sur [1,+ ∞ [ et f(1)=1-ln(1)=1. Donc x>1 Þ f(x)>1 c’est-à-dire x-1>ln(x).)

Appliquons cette inégalité. Si on se donne x>1, on peut appliquer à l’inégalité ln(y)<y. Cela donne , et donc . Quand x tend vers +∞ cela entraîne, par le théorème des gendarmes, qu’on a :

.

Pour x>0, on a x.ln(x)= -ln(1/x)/(1/x), avec 1/x tendant vers +∞ quand x tend vers 0⁺, donc :

.

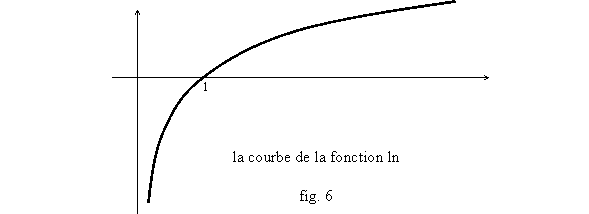
La première de ces limites exprime que, comme la fonction racine carrée, la fonction ln est de plus en plus petite par rapport à x : la courbe, bien que tendant vers +∞, « s’écrase » quand x devient grand, comme une parabole renversée (fig. 6). En fait, on le verra, cette courbe s’écrase « plus » que la vraie parabole renversée y=x^1/2, ou même que n’importe quelle courbe y=x^a avec 0<a<1, puisque le quotient ln(x)/x^a tend vers 0 quand x tend vers +∞ (ln(x) est « infiniment petit » devant x^a quand x tend vers +∞).

Comme ln tend vers +∞ en +∞, et vers -∞ en 0⁺, le théorème des valeurs intermédiaires prouve que, si on fixe n’importe quel nombre x, on trouvera au moins un UÎ]0,+∞[, tel que ln(U)=x. De plus ce U est unique, car ln étant strictement croissante, on aura ln(t)<ln(X)=y si t<X, et ln(t)>ln(U)=y si t>U. Donc ln(t)¹x si t¹U. Ainsi cette démarche permet de définir une nouvelle fonction, appelée fonction exponentielle, et notée exp : pour tout réel, exp(x) est l’unique réel strictement positif tel que ln[exp(x)]=x.

Exemple : exp(0)=1 puisque 1 est le réel tel que ln(1)=0.

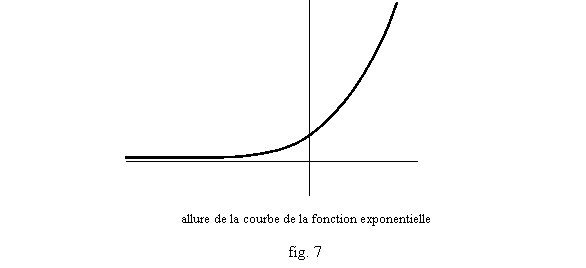
1^ère propriété : comme ln est strictement croissante, exp l’est aussi : en effet si x est un réel et y=exp(x), on a ln(y)=x. Soit x’>x. Un nombre positif z≤y vérifiera ln(z)<ln(y)=x<x’. Donc l’unique réel positif y’ tel que ln(y’)=x’ ne peut pas être ≤y. On a donc y’>y c’est-à-dire exp(x’)>exp(x). La fonction exponentielle est représentée fig.7.

2^ème propriété : on a pas seulement ln[exp(x)]=x pour tout x, on a aussi exp[ln(y)]=y pour tout y>0. En effet comme y est le nombre dont le logarithme est ln(y), par définition de l’exponentielle le nombre exp[ln(y)] est égal à y.

3^ème propriété : La relation ln(ab)=ln(a)+ln(b) se traduit pour cette nouvelle fonction. Si x,y sont deux réels, et si on pose exp(x)=a, exp(y)=b, par définition on a ln(a)=x, ln(b)=y, donc ln(ab)=x+y, ce qui prouve que l’exponentielle de x+y est ab=exp(x)exp(y) :

Pour toute paire de réels x,y, on a : exp(x+y)=exp(x)exp(y).

Conséquence : Cette relation permet de prouver :

exp(2x)=exp(x+x)=exp(x)exp(x)=[exp(x)]²,

exp(3x)=exp(2x+x)=exp(2x)exp(x)=[exp(x)]²exp(x)=[exp(x)]³,

etc.

En fait on a pour tout reel x>0, et tout entier naturel n, exp(nx)=[exp(x)]ⁿ.

Comme on a aussi x+(-x)=0, on peut écrire 1=exp(0)=exp[x+(-x)]=exp(x)exp(-x) ce qui prouve qu’on a : exp(-x)=1/exp(x).

En fin de compte, si n est un naturel, exp(-nx)=exp((-1)nx)=1/exp(nx)=1/[exp(x)]ⁿ=[exp(x)]^-n.

Enfin si x est un réel, n un entier et m un entier naturel non nul, on peut poser y=(n/m)x. Alors on aura m.y=m(n/m)x=n.x, donc on peut écrire : exp(my)=exp(nx), et [exp(y)]^m=[exp(x)]ⁿ, ce qui donne finalement : exp(y)=[exp(x)]^n/m, c’est-à-dire :

exp((n/m)x)=[exp(x)]^n/m

ou encore, si r=n/m est n’importe quel nombre rationnel,

exp(r´x)=[exp(x)]^r

En particulier si x=1, exp(r)=[exp(1)]^r.

On pose donc e=exp(1), et comme on a exp(r)=e^r pour tout rationnel, on étend la notation à tout réel, et on obtient :

Pour tout réel x, exp(x)=e^x.

Remarque : le nombre e ainsi défini, est un nombre irrationnel qui a en mathématique une importance comparable à celle du nombre p. On a e=2,7182818285… .

Par ailleurs la relation exp(r´x)=[exp(x)]^r vraie pour tout rationnel r et tout réel x donne, si a>0 et qu’on l’applique au nombre x=ln(a), qu’on a, pour tout rationnel r :

exp(r´ln(a))=[exp(ln(a))]^r=a^r puisque exp(ln(a))=a pour tout a>0.

On étend donc cette notation :

Pour tout réel x, et tout réel a>0, on notera a^x le nombre exp[x´ln(a)]=e^x´ln(a).

Les propriétés de la fonction exp assurent que les règles de calcul habituelles avec les puissances sont toujours valables. En particulier si a,b sont deux réels strictement positifs et si x,y sont des réels quelconques, on a :

a^x+y=a^xa^y ;

(a^x)^y=a^xy ;

(ab)^x=a^xb^x ;

a^-x=1/a^x ;

(a/b)^x=a^x/b^x.

Par ailleurs si a,x sont des réels positifs fixés, a¹1, l’équation en y : « a^y=x », qui s’écrit e^yln(a)=x, admet une unique solution, y, tel que y´ln(a)=ln(x) soit y=ln(x)/ln(a). Pour cette raison, les fonctions x a a^x et x a ln(x)/ln(a) s’appellent fonctions exponentielle et logarithme de base a, et sont parfois notées exp_a et log_a. Certaines sont très utiles : par exemple log₁₀, le logarithme de base 10, sert en chimie, en biologie, en physique, etc. Il donne des ordres de grandeur. Dire que log₁₀(A)=5 signifie que A=10⁵, dire que log₁₀(A) est entre 5 et 6 signifie que A est entre 10⁵ et 10⁶. On utilise ce log pour définir le pH, nombre sui donne l’ordre de grandeur de la concentration en ion H₃O⁺ d’une solution : pH@2 signifie une concentration de l’ordre de 10^-2, beaucoup d’ions H₃O⁺, pH@11 signifie une concentration de l’ordre de 10^-11, peu d’ions, etc.

Avec ces notations, les fonctions exp et ln sont les exponentielle et logarithme de base e.

On peut aussi, avec ces nouvelles définitions, étendre les fonctions puissances : si a est un réel quelconque, on appelle fonction puissance a la fonction notée x a x^a, définie sur R₊^* par :

x^a=e^aln(x).

Etudions maintenant la continuité et la dérivabilité de l’exponentielle. Reprenons la fonction log : si 1/2<t<2, on aura 1/2<1/t<2. D’après les inégalités des accroissements finis appliquées entre 1 et yÎ[1/2,2] à la fonction ln dont la dérivée est t a 1/t, on a donc :

Si 1/2≤y≤2, on a : 1/2|y-1|≤|ln(y)-ln(1)|≤2|y-1| soit, puisque ln(1)=0 :

1/2|y-1|≤|ln(y)|≤2|y-1|.

Soit x un réel entre -ln(2) et ln(2), et posons y=e^x. Alors 1/2≤y≤2, donc :

1/2|y-1|≤|ln(y)|≤2|y-1|.

Ce qui s’écrit :

1/2|e^x-1|≤|ln(e^x)|≤2|e^x-1|.

Et :

1/2|e^x-1|≤|x|≤2|e^x-1|.

On peut voir ces inégalités dans l’autre sens :

|x|≤2|e^x-1| Þ |x|/2≤|e^x-1|, et :

1/2|e^x-1|≤|x| Þ |e^x-1|≤2|x|.

Finalement on a obtenu :

Pour tout xÎ[-ln(2),ln(2)], on a : |x|/2≤|e^x-1|≤2|x|.

Quand x tend vers 0, el théorème des gendarmes assure donc que e^x-1 tend vers 0, donc que e^x tend vers 1=e⁰ : exp est continue en 0.

En fait si a et x sont deux réel quelconques, on a e^x=e^(x-a)+a=e^x-ae^a. Quand x tend vers a, x-a tend vers 0 et e^x-a tend vers 1 donc e^x tend vers e^a : la fonction exponentielle est continue en tout point.

Posons maintenant pour tout y>0, y distinct de 1, f(y)=ln(y)/(y-1). C’est le taux d’accroissement de la fonction ln, donc quand y tend vers 1, f(y) tend vers ln’(1)=1/1=1.

Or si x est un réel non nul, e^x est un réel positif distinct de 1, et on a :

quand x tend vers 0, ex tend vers 1, donc f(e^x) tend vers la limite de f(y) quand y tend vers 1, c’est-à-dire 1, et tend vers 1/1=1. Autrement dit :

.

Si a est un réel quelconque et x¹a, on peut écrire :

.

Ainsi, quand x tend vers a, x-a tend vers 0, donc tend vers 1 et finalement tend vers e^a´1=e^a. Conclusion :

En tout point a, la fonction exp est dérivable et exp’(a)=e^a=exp(a),

exp est sa propre fonction dérivée.

Pour en finir avec ces limites concernant la fonction exponentielle, on peut remarquer que l’inégalité ln(y)<y-1 vraie pour tout y>1 se traduit, en l’appliquant à y=e^x pour n’importe quel x>0, par : x<e^x-1 ou x+1<e^x. Il s’ensuit que e^x tend vers +∞ quand x tend vers +∞ :

.

On en déduit d’autres limites. Avec la formule e^-x=1/e^x on obtient :

.

Si on remarque que x/e^x=ln(e^x)/e^x, que , et si on compose les limites, on a :

.

Si n est un naturel quelconque, on a aussi, comme xⁿ/e^x=xⁿ/(e^x/n)ⁿ=nⁿ[(x/n)e^x/n]ⁿ :

.

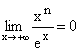Ce calcul montre comment on peut déduire de nouvelles limites. Par exemple on peut prouver que :

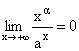dès que a>1, et 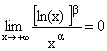dès que a>0.

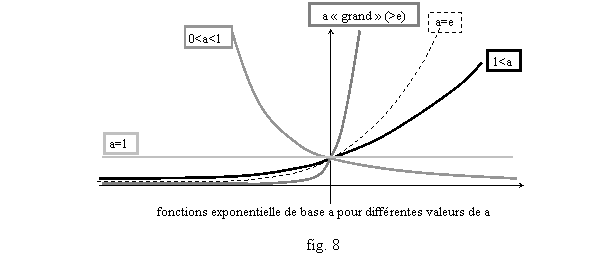
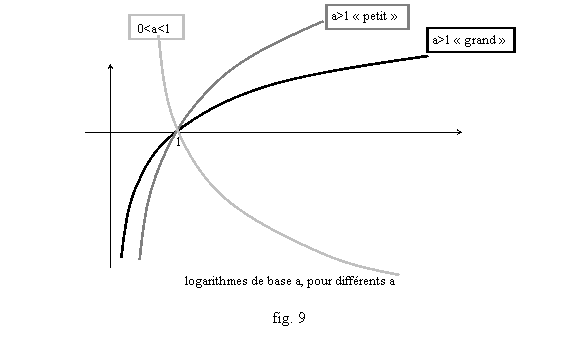
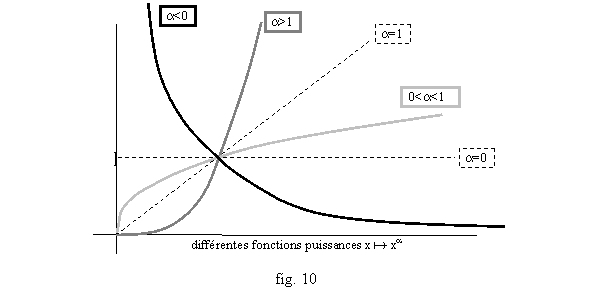
L’étudiant curieux s’amusera à démontrer ces formules, et étudiera aussi les sens de variations des autres fonctions exponentielles (fig. 8), logarithmes (fig. 9), puissances (fig. 10), en démontrant par compositions à partir des logarithme et exponentielle népériens leur dérivabilité et leur continuité, pour justifier ces dessins. En particulier on utilisera la formule de dérivée des composée pour prouver que x a x^a est dérivable sur R₊^* de dérivée x a ax^a-1.

Exercices :

1) Démontrer les formules suivantes :

cos(a)cos(b)=(cos(a+b)+cos(a-b)) ; sin(a)cos(b)=(sin(a+b)+sin(a-b)) ;

cos(a)+cos(b)=; sin(a)+sin(b)=.

2) Même question pour les formules :

cos(2a)=2cos²(a)-1=1-2sin²(a) ; sin(2a)=2sin(a)cos(a) ; cos(3a)=4cos³(a)-3cos(a).

3) De même pour : .

4) Utiliser les formules précédentes pour transformer en somme les produits suivants : sin²(x)cos(x) ; cos(x)cos(2x)cos(3x) ; sin³(x).

5) Utiliser les formules précédentes pour transformer en produit les sommes suivants : sin(x)+sin(2x) ; sin(x)+cos(x) ; cos(x)+cos(2x)+cos(3x) ; tan(x)+cos(x).

6) Soit x un réel qui n’est pas un multiple de p/2. On pose tan(x/2)=t. Etablir les formules :

; ; .

7) En utilisant des propriétés géométriques simples, établir que :

 ;  ;  ;

 ;  ;  ;

 ;  ; .

8) Calculer tan(3p/4) ; sin(5p/6) ; cos(2005p/3).

9) Ecrire des équations de degré 2 vérifiées par cos(p/12) et sin(p/12), et les calculer.

10) Transformer les sommes suivantes en expressions du type Acos(x+b) : cos(x)+sin(x), cos(x)+sin(x). En déduire les solutions de l’inéquation : cos(x)+sin(x)<.

11) Prouver les inégalités suivantes, en utilisant le théorème des accroissements finis :

pour tous x,y, |sin(x)-sin(y)|£|x-y| ; |cos(x)-cos(y)|£|x-y| ; pour tout x³0, sin(x)£x.

pour tous x,y strictement entre -p/2 et p/2, |tan(x)-tan(y)|³|x-y|.

12) Calculer les dérivées des fonctions suivantes : e^x2 ; ln(x+1) ;  ; sin(x)cos(x).

13) Soit f une fonction ne s’annulant pas sur un intervalle I. On pose L(x)=ln|f(x)|. Etudier la dérivabilité de L et la valeur de L’. Quels liens y a-t-il avec l’exercice 3, paragraphe 1 ?

14) Calculer la dérivée des fonctions suivantes, en étudiant d’abord les domaines de définition et de dérivabilité : ln|sin(x)| ; ln|tan(x)| ; ln|cos(x)|.

15) Déduire de l’inégalité : 1/x²<1/x<1, vraie si x<1, qu’on a aussi : (x-1)/x<ln(x)<x-1 si x>1. Utiliser ceci pour prouver que : 0,5<ln(2)<1.

16) On pose f(x)=xe^x. Prouver que f atteint un minimum absolu en x= -1.

17) On pose f(x)=e^x-x². Calculer la dérivée g(x)=f’(x), puis la dérivée de la dérivée, g’. Montrer que g atteint un minimum absolu en x=ln(2), et que g(ln(2))>0. Que dire du sens de variation de f ? Donner l’allure de son graphe.

18) On pose f(x)=e^x-5x². Calculer la dérivée g(x)=f’(x), puis la dérivée de la dérivée, g’. Montrer que g atteint un minimum absolu en x=ln(10), et que g(ln(10))<0. Que dire des variations de f ? Donner l’allure de son graphe, et le nombre de solution de l’équation f(x)=0.

19) Reprendre les idées des exercices précédents pour les fonctions suivantes : f(x)=e^x-x ; f(x)=e^x-ex ; f(x)=e^x-2005x ; f(x)=e^x-x³ ; f(x)=e^x-x^e.

20) Calculer les limites suivantes :

 ;  ;  ;  ; .

21) Mêmes questions avec :

 ;  ; .

22) On fixe un paramètre a et on pose f(x)=x^a pour x>0. on pose si x¹1. Que vaut la limite  ? Montrer que, pour x>0, on a : f(x+1)-f(x)=x^a-1g(1+1/x). En déduire la valeur des limites de f(x+1)-f(x) et de [f(x+1)-f(x)]/x^a-1 quand x tend vers +∞.