Mathématiques

Cours-TD – Culture Scientifique de base – 2005-2006

Chapitre 1 - Généralités sur les fonctions réelles de la variable réelle.

Dans l’unité de « Culture Scientifique de base », on étudie essentiellement la notion de fonction réelle de variable réelle. C’est une notion qui sert à exprimer comment évolue une grandeur dépendant d’une variable – comme le temps, une concentration, une intensité électrique, etc. – et qui du coup est utile dans de nombreuses disciplines, notamment dans les disciplines scientifiques présentes dans le « tronc commun ». En mathématique, on doit partir du minimum de connaissances, de présupposés, et procéder à une démonstration de chaque nouvelle propriété. Néanmoins, pour ne pas alourdir le cours et pour pouvoir aborder rapidement les techniques utiles de calculs et d’études des fonctions, nous allons procéder autrement pour commencer. Le présent chapitre contiendra donc peu de démonstrations, elles seront refaites plus tard, pour ceux qui choisiront le parcours mathématique par exemple. Les étudiants doivent donc croire ce qui leur est exposé ci-après, grâce à leur confiance dans la bonne foi des professeurs. Les affirmations qui seront ainsi « admises » concernent des objets ou des notions que beaucoup ont déjà étudiés au lycée : fonctions continues, calculs de base sur les réels ou les fonctions, fonctions usuelles (exponentielles et logarithmes, trigonométrie, chapitre 2). À partir du chapitre 2 et de la notion de dérivée, on s’efforcera de démontrer toute nouvelle affirmation. Le « gros » du programme des 6 premières semaines tourne autour de cette notion, et de son utilisation pour étudier les variations des fonctions (tableaux de variation, représentations graphiques, etc.)

1) Rappels sur les réels.

Les nombres utilisés sont les nombres réels, éléments de l’ensemble R. On utilisera les sous-ensembles usuels de R : l’ensemble des réels positifs R₊, des réels strictement positifs R₊^*, des réels négatifs et strictement négatifs R_- et R_-^*, des réels non nuls R^*, et les autres ensemble de nombres particuliers : nombres entiers naturels (0, 1, 2, 3, etc. ; c’est l’ensemble N), nombres entiers relatifs (les naturels et leurs opposés -1, -2, -3, etc. ; c’est l’ensemble Z), ainsi que, à l’occasion, les nombres rationnels (les quotients d’entiers p/q, comme les entiers n=n/1, les inverses 1/2, 1/3, etc., les autres quotients 2/3, -5/4, etc. ; c’est l’ensemble Q). On connaît aussi l’ensemble vide, noté Æ.

Les nombres réels sont représentés sur une droite graduée, et on parlera parfois de « points » sur la droite au lieu de « nombres » (cf. fig. 1). Il est facile d’y représenter aussi les entiers naturels ou même les entiers relatifs (ils sont marqués fig. 1 : cela correspond juste à la graduation de la droite dessinée). En revanche on ne peut isoler facilement les rationnels, car ils se retrouvent « partout ». On connaît les opérations usuelles entre nombres réels : addition, soustraction, multiplication, division ; on connaît les règles de calculs relatifs aux puissances : x², x³, etc. On se souviendra qu’un carré x² est toujours positif, et réciproquement si a est un réel positif, il existe deux réels opposés dont le carré vaut a (ou un seul, égal à 0, si a=0) ; le réel positif x tel que x²=a se note et s’appelle la racine carrée de a.

La représentation graphique des réelles est en général utile pour mieux cerner les problèmes, et parfois pour les résoudre. Ainsi on connaît les relations classiques de « comparaisons » entre nombres : plus petit que, strictement plus petit que, plus grand que, etc. On sait que les ensembles des réels positifs ou strictement positifs sont utiles pour formuler ces relations. Ainsi on a, si x et y, sont deux réels :

« x est inférieur ou égal à y » (x≤y, on dit plus simplement « x est inférieur à y », ou « x est inférieur à y au sens large ») si et seulement si y-x est un réel positif ou nul.

« x est strictement inférieur à y » (x<y, on dit aussi « x est inférieur à y au sens strict ») si et seulement si y-x est un réel strictement positif.

Pour éviter les ambiguïtés, il est préférable de toujours préciser « strictement » ou « au sens large ».

Ces relations servent à définir d’importants sous-ensembles de R, les intervalles. C’est aussi une première illustration de l’utilisation des dessins pour représenter R et ses sous-ensembles. Sur le dessin, on retrouve x<y dans le fait que x est à gauche de y sur R (fig. 2). On ne peut pas marquer de manière nette et différente la relation x≤y.

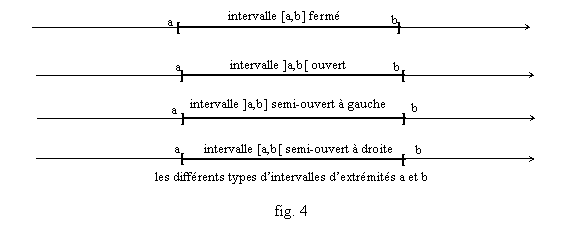
Si a et b sont deux nombres réels, l’intervalle fermé borné [a,b] est l’ensemble des réels qui sont entre a et b, au sens large, c’est-à-dire les nombres x tels que a≤x≤b. D’après le dessin de la figure 2, si a<b, l’intervalle [a,b] doit être représenté par le segment de droite reliant le point qui représente le nombre a et le point qui représente le nombre b (fig. 3, pour cette raison on appelle aussi cet intervalle le « segment [a,b] »). Si a>b, l’intervalle est l’ensemble vide Æ. Et si a=b, l’intervalle [a,a] ne contient que le nombre a.

De même on appelle intervalle ouvert d’extrémités a et b, et on note ]a,b[, l’ensemble des nombres x tels que a<x<b. Il est non vide si a<b. Il y a aussi les intervalles semi-ouverts (on dit aussi semi-fermés) : l’intervalle ]a,b] semi-ouvert à gauche, ensemble des x tels que a<x≤b, et l’intervalle [a,b[ semi-ouvert à droite, ensemble des x tels que a≤x<b. Sur le dessin, on ne peut pas aisément faire la différence entre les intervalles ouverts, fermés, semi-ouverts. Aussi on utilise en général un symbole représentant l’ouverture ou la fermeture, par exemple, comme on fera dans ces polycopiés, un crochet (fig. 4).

Ces intervalles sont appelés intervalles bornés. Les nombres a et b sont leurs bornes. Les intervalles qui n’ont qu’une borne, un réel a, et sont « illimités » d’un côté, sont dits non bornés. Il y a les intervalles non bornés à gauche, l’intervalle ouvert ]-∞, a[ – ensemble des x tels que x<a, et l’intervalle fermé ]-∞,a], ensemble des x tels que x≤a (fig. 5). Et puis les intervalles non bornés à droite, ]a,+∞[ ou [a,+∞[.

On peut aussi remarquer que R est un intervalle, sans borne, qu’on peut noter ]-∞,+∞[. Cette façon de voir est utile, car on peut aussi trouver un point commun à tous les intervalles de R : ce sont les sous-ensembles de R qui sont « d’un seul morceaux », « sans trous », c’est-à-dire qu’on ne peut pas trouver trois nombres u,v,w qui se suivent, tels que u<v<w, et que u, w soient dans l’ensemble, mais pas v. Quand on cherche tous les sous-ensembles de R ayant cette propriété, on trouve exactement les neufs types d’intervalles qu’on a énumérés ci-dessus, les 4 types bornés (parmi lesquels Æ), les 4 types non bornés, et R tout entier (fig. 6).

La première fois qu’on rencontre les intervalles, c’est pour tout un tas de problèmes classiques, que les étudiants ont sûrement déjà eu à résoudre : les inéquations. On part d’une inégalité (souvent issue d’un calcul : comment faire mes courses quand je n’ai que 100 F, comment charger mon camion qui doit porter moins de 2 tonnes, quels appareils brancher sur mon circuit dont je connaît l’ampérage maximum supporté, etc.…). Quand cette inégalité contient une variable dont la valeur est inconnue, résoudre cette inégalité veut dire la remplacer par des inégalités équivalentes, c’est-à-dire vérifiées pour les mêmes valeurs de x, exprimant simplement les conditions que doivent vérifier x. En pratique, cela signifie que les solutions sont les nombres x qui sont dans tel intervalle. Parfois on a une solution du type : « x est solution si et seulement si x est dans tel premier intervalle, ou dans tel second, ou dans tel troisième, etc.… » Ceci s’exprime en disant que x doit être dans l’ensemble formé par la réunion de l’intervalle 1, de l’intervalle 2, de l’intervalle 3, etc. Pour écrire ces conditions, on donne deux symboles utiles :

- le symbole d’appartenance, xÎE signifie que x est élément de l’ensemble E, par exemple xÎ[0,2[ signifie que x est élément de [0,2[, ou encore que 0≤x<2. Ces conditions sont des synonymes, elles sont « équivalentes ».

- le symbole de réunion : EÈF désigne l’ensemble des éléments qui sont soit dans E, soit dans F.

Par exemple [0,2[È[4,5] (fig. 7) est l’ensemble des x qui vérifient soit 0≤x<2, soit 4≤x≤5 (c’est un ensemble avec un trou, puisque 0ÎEÈF et 4ÎEÈF. Mais 3 n’est pas dans EÈF).

Autre exemple : [0,2[È[1,5]=[0,5] (fig. 7).

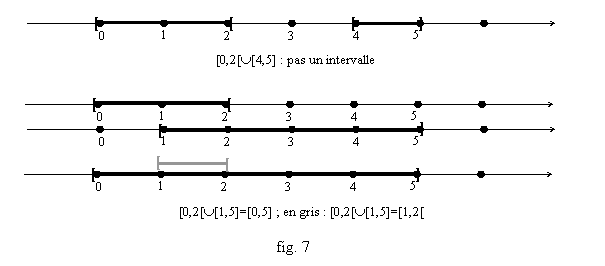
Signalons aussi le symbole Ï qui signifie « n’appartient pas », pour dire qu’un élément n’est pas dans un ensemble, et le symbole Ç qui se lit « inter » et signifie « intersection » : EÇF est l’ensemble des éléments qui sont à la fois dans E et dans F ; par exemple [0,2[Ç[1,5] est l’ensemble des x qui vérifient à la fois 0≤x<2 et 1<x≤5, c’est-à-dire ceux qui vérifient 1<x<2, autrement dit l’intervalle ouvert [1,2[. On écrira [0,2[Ç[1,5]=[1,2[ (fig. 7).

Par exemple si on veut trouver à quelle condition sur le réel x on a : 2x+1>0, on peut procéder comme suit :

Pour tout réel x, l’inégalité « 2x+1>0 » est vraie si et seulement si on a : « 2x>-1 » (car on peut rajouter le même nombre, ici -1, aux deux côtés d’une inégalité, on obtient une inégalité équivalente).

Ensuite pour tout réel x, « 2x>-1 » est vraie si et seulement si « x>-1/2 » (car on peut multiplier par un même nombre strictement positif les deux côtés d’une inégalité, on obtient une inégalité équivalente ; on rappelle que si on veut multiplier par un réel strictement négatif, il faut inverser le sens de l’inégalité).

On a donc « résolu » l’inéquation : on l’a transformée sous une forme où on voit directement que x vérifie l’inéquation si et seulement si x>-1/2, c’est-à-dire que l’ensemble des solutions est l’intervalle ]-1/2,+∞[.

Quand on transforme une inégalité en une inégalité équivalente, on sous-entend toujours que la transformation est vraie « pour tout réel x ». On peut rédiger autrement : on fixe un réel x particulier, et alors on part de la première ligne (qu’on aimerait bien que x vérifie) et on transforme en écrivant des inégalités équivalentes, pour ce x.

On donne les notations suivantes :

Pour dire que deux écritures sont équivalentes, on utilise le symbole : Û , qui se lie « si et seulement si », ou « est équivalent à ».

La résolution de l’inéquation ci-dessus s’écrira par exemple :

Fixons un réel x. On a alors : 2x+1>0 Û 2x>-1

Û x>-1/2.

Si une inégalité (A) est la conséquence obligatoire d’une autre inégalité (B), on dit que (B) « implique » ou « entraîne » (A), ce qu’on note : (B) Þ (A). Les deux ne sont pas forcément équivalentes (si on peut avoir (A) sans avoir (B)).

Par exemple, cherchons la solution à l’inéquation : .

Soit x un réel. Alors :

(x-2 est défini et ).

Un x qui serait solution vérifierait donc forcément . Par ailleurs si x-2 est défini, on aura : . On peut donc écrire, pour tout réel x :

Supposons que x soit solution : cette hypothèse, et l’implication précédente, montre que x vérifie : x-2<1. Or :

x-2<1 Û x<3.

Ainsi une solution x à l’inéquation doit vérifier x<3. Mais on n’a pas transformé l’inégalité de départ par des équivalences, rien ne garantit que tous les réels x tels que x<3 soient solutions.

En fait, pour que l’expression soit définie, il faut qu’on ait x-2 positif, x-2≥0 donc x≥2. Autrement dit si x est solution, on a 2£x et x<3, c’est-à-dire xÎ[2,3[. Maintenant, on peut vérifier que ces nombres conviennent : si 2≤x<3 alors 0≤x-2<1 et on a bien : . L’étape de vérification est obligatoire, si on se contente d’écrire , on n’a pas trouvé l’ensemble des solutions : par exemple 0<3, mais 0 n’est pas solution puisque n’est même pas défini.

Pour tous ces calculs, il faut posséder connaissances du lycée, notamment les règles de transformations des égalités et inégalités. Ce savoir faire sera précieux en SFE1. Il faut aussi connaître les « identité remarquable » :

Quels que soient les réels a et b :

(a+b)²=a²+2ab+b².

(a-b)²=a²-2ab+b².

a²-b²=(a-b)(a+b).

Pour finir ce tour d’horizon, on introduit une notation utile :

Partons d’une suite finie de réels, c’est-à-dire un nombre N de réels qu’on a « numérotés » en portant en général le numéro en indice : x₁, x₂, …x_N, (il peut s’agir d’une formule de calcul qui donne x_k en fonction de k). On a une notation spécifique pour désigner leur somme : x₁+x₂+…+x_N se note . On lit ceci « somme, de k égal 1 à k égal N, du terme x_k » (ou simplement « de x_k »). Le symbole S (lettre grecque sigma majuscule) se nomme, dans ce contexte, le « signe somme ».

Dans cette écriture la lettre k n’a aucune importance, elle ne sert qu’à noter qu’on fait la somme de tous les termes, et elle peut être remplacée par n’importe qu’elle autre lettre, à part N, qui a une existence hors de la somme puisque c’est le nombre, déjà fixé avant (en principe !), de termes de la suite. On dit que k est une variable muette. Bien sûr la somme peut commencer à un autre indice que l’indice 1 : 0, ou un autre nombre (éventuellement figuré par une lettre, à condition que la lettre soit définie ailleurs).

Exemple : soit N un entier. On pose S=. Calculer S en étudiant, pour tout entier k, la différence (k+1)²-k².

(Dans la fin de la question, on a pris la lettre k pour rappeler la notation de la somme, et suggérer qu’il faudra additionner les égalités trouvées. Mais on pourrait remplacer la lettre k du signe somme par x, t, j, p, etc. : cela ne changerait pas la question.)

S n’est autre que la somme des N premiers entiers, qu’on pourrait écrire (1+2+…+N).

Prenons k un entier quelconque. D’après les identités remarquables, on a :

(k+1)²-k²=(k²+2k+1)-k²=2k+1.

Si on additionne le nombre x_k=(k+1)²-k²=2k+1 de k=1 à k=N, on obtient :

On peut alors transformer plusieurs écritures : une somme d’une suite obtenue par addition de termes y_k+z_k est égale à la somme des y_k plus la somme des z_k. De même si A est un nombre fixe, la somme des nombres A.y_k est égal à A fois la somme des y_k. Ces règles proviennent des règles :

(y+z)+(y’+z’)=(y+y’)+(z+z’), et (A.y)+(A.y’)=A(y+y’).

Mais au lieu de les appliquer pour des sommes de deux éléments y+y’, z+z’, on les applique pour des sommes de 3, 4, jusqu’à N nombres. Ce qui donne :

et .

Ceci étant dit on a : . Par ailleurs on peut calculer de deux manières. En remarquant que cette somme s’écrit :

[2²-1²]+[3²-2²]+[4²-3²]+… +[N²-(N-1)²]+[(N+1)²-N²]=(N+1)²-1²=N²+2N+1-1=N²+2N.

car dans cette somme, chaque terme positif 2², 3², etc., jusqu’à N², se simplifie avec le terme négatif qui suit, -2², -3², …, -N².

Si on veut faire ce calcul on peut garder la notation « somme » :

or la somme est égale à . En effet quand l’entier k va de la valeur 1 à la valeur N, l’entier j=k+1 prend toutes les valeurs possibles d’entiers, entre 2 et N+1. Ensuite il suffit de remplacer la lettre j par la lettre k, c’est possible puisque la lettre figurant dans la somme n’est qu’un symbole d’écriture : . On a la différence de deux sommes ayant presque tous les termes en commun. On peut donc écrire : , et aussi . En fin de compte on a :

Quelle que soit la méthode, le résultat est le même. Par ailleurs on a aussi : . En effet cette somme s’écrit (1+1+…+1) avec N terme, donc vaut N. On peut aussi remarquer que (k+1)-k=1 pour tout k, donc la somme calculée s’écrit :

par un calcul analogue à celui effectué pour les carrés.

Si on résume l’égalité :

s’écrit :

d’après les calculs précédents, donc on obtient :

2S=N²+N, donc :

.

Bien sûr il faut manier ces symboles pour s’habituer à leur usage. Notons que les écritures traditionnelles avec « petits points » peuvent être source d’erreurs dans les calculs, même si elles sont utiles pour aider l’intuition. Par exemple on peut vérifier sur des valeurs particulières que la formule précédente est vraie :

(1+2)=(2´3)/2=3, (1+2+3)=(3´4)/2=6, (1+2+3+4)=(4´5)/2=10, (1+2+3+4+5)=(5´6)/2=15,…

Les nombres 3, 6, 10, 15 sont de plus en plus grands et croissent de plus en plus vite. Pourtant que penser de ce raisonnement :

« On note S la somme des entiers de 1 à N, et S’ la somme des entiers de 1 à N+1. Alors on a :

S=(1+2+…+N). Ajoutons 1 des deux côtés, on obtient :

(S+1)=(1+2+…+N)+1=(1+2+…+N+1)=1+2+…+(N+1)=S’.

On aura donc à chaque fois S’=S+1. »

On a S=1+2=3 quand N=2, donc S’=1+2+3 devrait valoir 3+1=4, et 1+2+3+4 devrait valoir 4+1=5, etc. D’où vient l’erreur ?

En fait, dans la parenthèse (1+2+...+N)+1, la somme se termine par …+(N-1)+N. Si on rajoute 1 à N, on obtient donc (1+2+…+(N-1)+N)+1=(1+2+…+(N-1))+(N+1). Cette somme n’est pas égale à S’, puisque dans S’ il y a le terme N : S’=1+2+…+(N-1)+N+(N+1). C’est la notation avec les « … » qui a causé l’erreur, car on ne voyait pas les derniers termes de la somme avant N. Une notation avec le signe « somme » empêche – en principe – ce genre de confusion.

En plus du signe « somme », on rencontrera aussi le signe « produit » : P. Il s’agit de noter le produit d’une suite finie de nombres réels, désigne le produit x₁´x₂´…´x_N (la lettre k est une variable muette, comme pour les sommes, le fonctionnement en est le même).

Exemple : Si N est un entier, calculer le produit .

On remarque que pour tout entier k³1 on a : . On reporte cette expression dans P :

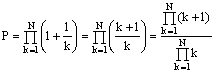
grâce aux règles de calculs (, généralisées avec N quotients).

Ensuite si on pose j=k+1, j prend toutes les valeurs entières entre 2 et N+1 quand k va de 1 à N. On peut donc transformer le produit, puis dans un deuxième temps remettre la lettre k à la place de la variable j, puisque ce sont des variables muettes.

On a donc : .

La dernière transformation vient de ce qu’on a séparé le produit de tous les entiers de 2 à N+1 en le produit des entiers de 2 à N, fois N+1.

De même on a : . Finalement on trouve :

.

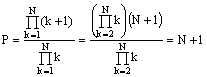Là encore, avec un peu d’habitude, il faudra aller plus vite.

Signalons pour conclure un symbole très utile pour de nombreuses formules, défini au moyen d’un produit :

Si N est un entier naturel, on appelle factorielle N le nombre, noté N !, égal à 1 si N=0, et égal au produit suivant si N≥1 :

.

Exercices

1)- Résoudre les équations suivantes en x dans R :

x²=2x-1 ; x³+x=2x² ; x²+2x-3=0 ;  ; .

2)- Résoudre les inéquations suivantes, en x dans R :

3x+1>1-2x ;  ;  ; 1/x+1/(x+1)<0 ; .

3)- Si a et b sont deux réels quelconques, développer les expressions : (a+b)³ ; (a-b)³ ; (a+b)⁴.

4)- On utilisera les résultats du 3 :

a) quand k est un entier quelconque, développer (k+1)³-k³.

b) Déduire du a) la valeur de .

5)- En utilisant les résultats du 4)- et ceux donnés dans le cours, calculer les sommes suivantes :  ;  ; .

6)- Imaginer une méthode pour calculer - et effectuer le calcul.

7)- On fixe un entier N. Résoudre l’équation en x dans R : .

8)- On fixe un entier N. Résoudre l’équation en x dans R : (utiliser le résultat du 4)-).

9)- Prouver que, pour tout entier N≥1, on a : .

10)- Calculer les produits suivants, N étant un entier naturel non nul :  ;  ;  ;  ; .

11)- Résoudre dans R l’inéquation x(x+1)(x+2)(x+3)>0, en représentant l’ensemble solution sur un dessin.

12)- Même question avec l’inéquation : , N étant un entier naturel fixé.

2) Rappels sur les fonctions.

Les fonctions sont des correspondances d’un sous-ensemble de R dans R. Elles servent souvent à représenter comment une grandeur varie en fonction d’une autre, appelée la variable. Par exemple si un point se déplace sur une droite graduée, on peut étudier son mouvement en regardant comment varie son abscisse x en fonction du temps. Il faut prendre une origine du temps et alors, à chaque « date » t (en années, mois, jours, heures, minutes, secondes, etc.), correspond une abscisse x, qui indique à quel endroit était le point étudié (par exemple : centre de gravité d’une voiture, curseur du thermomètre, etc.). On obtient ainsi une fonction qui à tout t associe le nombre correspondant, qu’on notera x(t). De la même façon si on regarde une route, qui partirait par exemple de Caen, on peut mesurer l’altitude en suivant cette route. Si on écrit l’altitude h en fonction de la distance x parcourue depuis le départ, on obtient une fonction h(x). Les exemples sont multipliables à l’infini, et c’est ce qui fait l’utilité de la notion de fonction, et de l’étude de cette notion en général, sans se soucier si la fonction à laquelle on appliquera nos résultats représentera une position en fonction du temps, ou une température en fonction d’une position, ou une somme d’argent en fonction d’une masse, etc.

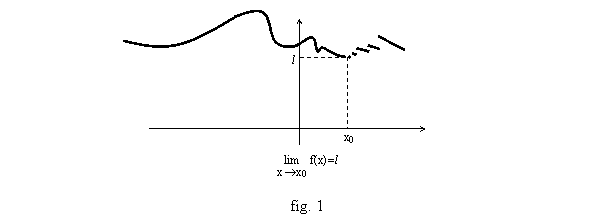
Soit f une fonction. Chaque réel a au maximum une « image », un nombre x avec lequel il est en correspondance, par f ; s’il n’en a pas, on dit que f n’est pas définie en ce nombre, et s’il en a on note f(x) l’unique image de x par f. L’ensemble des x où f(x) est définie s’appelle ensemble de définition de f et se note D_f. On représente souvent la fonction par son graphe.

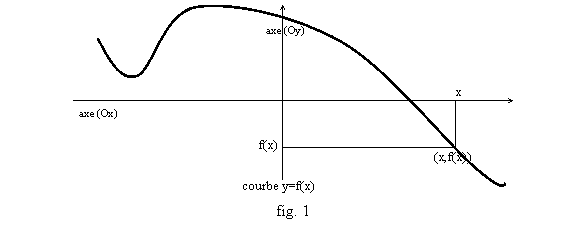
On choisit un repère du plan, de préférence orthogonal (axes orthogonaux), et le graphe de f est la courbe regroupant tous les points dont les coordonnées s’écrivent (x ; f(x)) pour un réel x, c’est-à-dire l’ensemble des points dont l’ordonnée est l’image de l’abscisse par f (fig. 1), qui sont tels que y=f(x), si y est leur ordonnée et x leur abscisse.

On retiendra des fonctions d’un usage courant :

Les fonctions constantes, telle que f(x) garde toujours une même valeur C (valeur de la constante, fig. 2.).

La fonction identité, telle que f(x)=x pour tout x (fig. 3). On la note Id cette fonction.

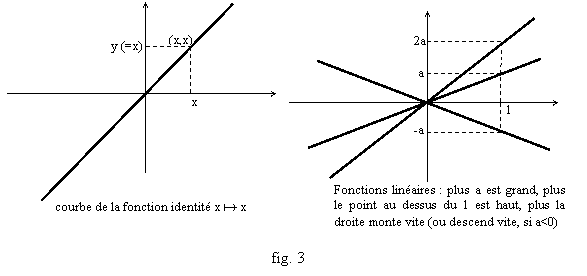
On connaît aussi les fonctions linéaires, obéissant à une formule du type f(x)=ax pour un réel a fixé, dont les graphes sont les droites passant par l’origine du repère. Plus a est grand en valeur absolue, plus la droite est penchée (fig. .3), puisque f(1)=a donc si on double a, le point au-dessus de l’abscisse 1 est deux fois plus haut (ou plus bas si a<0). Le cas a=1 donne Id.

On connaît plus généralement la classe de fonctions dont les courbes sont les droites non verticales : les fonctions affines. Une fonction affine est une fonction f, définie sur R, telle que f(x) se calcule à partir de x par une formule du type f(x)=ax+b, avec deux nombres fixes a, b. Le nombre a s’appelle le coefficient directeur de la fonction, ou de la droite qui est le graphe de la fonction. On parle aussi de la « pente » de cette droite. Comme f(0)=a´0+b=b, b s’appelle l’ordonnée à l’origine.

Remarquons que si f est cette fonction affine, et si x, y, sont deux réels, on a :

f(y)-f(x)=(ay+b)-(ax+b)=(ay-ax)+(b-b)=a(y-x).

Autrement dit l’écart entre f(y) et f(x) est égal à a fois l’écart entre y et x. On a par exemple f(x+1)=a(x+1)+b=ax+a+b=(ax+b)+a=f(x)+a ; f(x+2)=a(x+2)+b=ax+b+2a=f(x)+2a ; plus généralement si h est un réel, f(x+h)=a(x+h)+b=ax+ah+b=f(x)+ah. Autrement dit, si on augmente la variable x d’un certain nombre h, la valeur de f, f(x+h), augmente de ah – c’est-à-dire « a fois plus vite ».

Pour une fonction donnée f, on appelle taux d’accroissement de f entre deux nombres distincts x et y le nombre . D’après les calculs précédents, si f est une fonction affine de coefficient directeur a, ce taux est toujours égal à a. On peut donc faire ce calcul à rebours : partons de deux points A, B, dont les coordonnées sont notées (comme d’habitude) (x_A,y_A) et (x_B,y_B), et qui ne sont pas à la verticale l’un de l’autre, donc tels que x_A≠x_B. Une fonction f dont le graphe doit passer par A et B doit vérifier f(x_A)=y_A, f(x_B)=y_B. Le taux d’accroissement entre ces deux points est donc : =a. C’est donc le coefficient directeur de la droite qui passe par A et B. La fonction affine correspondante s’écrit f(x)=ax+b, et pour déterminer b, on peut par exemple remarquer que f(x_A)=y_A donc ax_A+b=y_A et b=y_A-ax_A.

C’est la détermination de a qui est souvent le plus important. Supposons que B soit « à droite » de A, c’est-à-dire x_B>x_A. Alors la différence x_B-x_A est positive, et le signe de a= est le signe de y_B-y_A. Si y_B-y_A>0, c’est-à-dire si B est « au dessus » de A, le coefficient directeur a est strictement positif. Les droites « montantes » sont celles qui ont un coefficient directeur strictement positif. De plus, si A et x_B sont fixés, on voit que plus y_B est grand – c’est-à-dire plus B est « haut » – et plus le coefficient a est grand : les droites montent d’autant plus vite que leur coefficient directeur est important. Ceci généralise les observations faites sur les fonctions linéaires, cas particulier (b=0) des fonctions affines.

droite y=2x+…

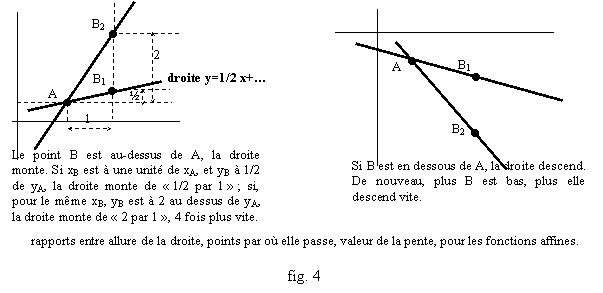
Inversement si B est en dessous de A, ou y_B<y_A, alors le coefficient est négatif, et par ailleurs plus B est bas, c’est-à-dire plus y_B est petit, plus a sera petit aussi (négatif mais grand en valeur absolu) : les droites descendent d’autant plus vite que leur coefficient directeur est grand en valeur absolu. Toutes ces considérations sont illustrées par la fig. 4.

Si A et B sont à la même hauteur – c’est-à-dire si y_A=y_B, on obtient : y_B-y_A=0 donc a=0, et f s’écrit f(x)=0x+b=b (avec b=y_A=y_B), on retrouve les fonctions constantes (fig. 2) : leurs graphes sont les droites horizontales.

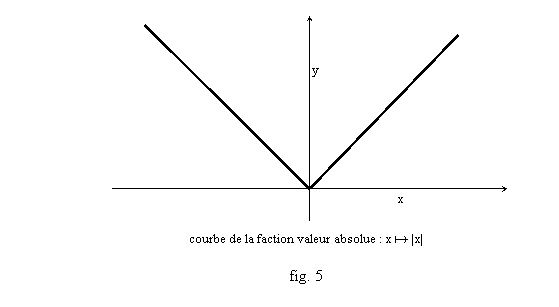
On retiendra aussi la fonction valeur absolue (fig. 6), notée |x| : |x|=x si x≥0, |x|=-x si x<0. C’est une fonction dont les valeurs (les images) sont prises dans R₊. Sa courbe est identique à la courbe de la fonction identité sur la partie du plan où x≥0 (à droite de l’axe des y), et identique à la courbe de la fonction affine x a -x sur la partie où x≤0 (à gauche de l’axe des y). Il faut s’habituer à son usage, et notamment dans les inégalités et inéquations.

Exemple : résoudre l’inéquation |x-1|<3.

Cette inéquation s’écrit |x-1|-3<0.

Partons d’un réel x quelconque.

Si x≥1, |x-1| vaut x-1, et |x-1|-3=x-1-3=x-4, qui est strictement négatif quand x<4, et positif sinon.

Si x≤1, |x-1| vaut –(x-1)=1-x, et alors |x-1|-3=1-x-3= -2-x, qui est strictement négatif si -2<x, et positif sinon. On peut résumer ceci dans un tableau :

-∞	-2	1	4	+∞
|x-1|-3=	-2-x		x-4
x-4		-	0	+
-2-x	+	0	-
|x-1|-3	+	0	- 0	+

Sur le tableau on voit dans quel colonne doit être le réel x pour vérifier |x-1|<3. L’ensemble des réels solutions est donc l’intervalle ]-2,4[.

Comme toujours, c’est l’habitude qui aide à maîtriser ces calculs. Notons que ces calculs sont utiles dans le contexte des études de fonctions. En effet quand on nous donne une formule prétendant définir une fonction, on doit fréquemment résoudre des équations ou inéquations, pour déterminer l’ensemble de définition de f.

Par exemple : Déterminer l’ensemble de définition de la fonction f, définie par la formule :

.

Pour un réel x fixé, le nombre f(x) est défini si la racine est calculable, soit 3-|x-1|≥0, et non nul pour pouvoir calculer son inverse. D_f est donc l’ensemble des x tels que 3-|x-1|>0. On est ramené à l’inéquation précédente, qu’on a déjà résolue : D_f est donc l’ensemble des solutions de cette inéquation, D_f=]-2,4[.

Il faut aussi connaître la fonction partie entière (fig. 6), notée E(x) ou [x] : [x] est le plus grand

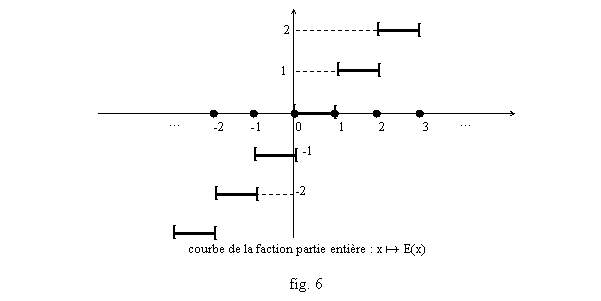
entier qui soit inférieur ou égal à x, donc [x]=0 sur l’intervalle [0,1[, [x]=1 sur l’intervalle [1,2[, [x]=2 sur [2,3[, [x]=-1 sur [-1,0[, [x]=-2 sur [-2,-1[, etc. Ainsi E(0,5)=0, E(3,14159265…)=3, E(-1,5)=-2. Pour tout x, on peut aussi dire que n=E(x) est l’unique entier tel que n≤x<n+1.

Moins élémentaires, les fonctions polynômes sont aussi à connaître, au moins pour savoir calculer avec : on ne rencontrera en général que des fonctions polynômes de petits degrés.

Il y a d’abord les fonctions puissances : x a xⁿ pour tout x, où n est un entier positif donné.

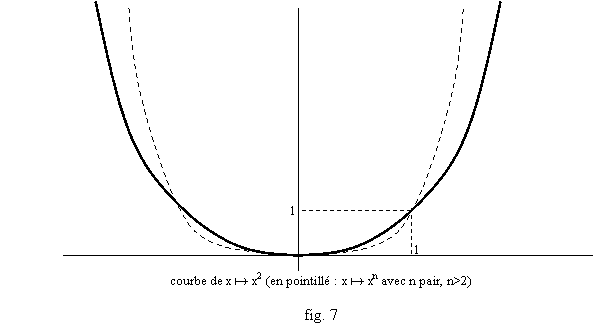
Il faut avoir une idée « qualitative » du graphe de ces fonctions. Ainsi pour n=0, x⁰=1, on retrouve une fonction constante, pour n=1, xⁿ=x, on retrouve la fonction identité ; pour n=2, xⁿ=x², la fonction « x au carré », a pour graphe une « parabole » (fig. 7), fonction qui augmente de plus en plus vite, et dont la courbe est symétrique par rapport à l’axe des y.

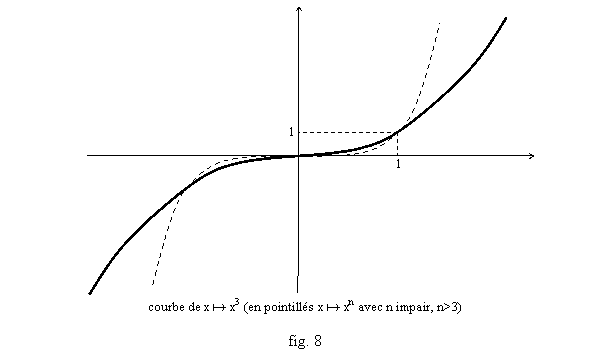
Pour n=3, xⁿ=x³, fonction « x au cube », le graphe (fig. 8) est, à droite de l’axe des y, comme celui de x², mais augmentant plus vite, et à gauche de l’axe des y, pour les x négatifs, on a x³≤0, la courbe est symétrique par rapport à l’origine du repère. Pour les n plus grands, et pairs, xⁿ est similaire à x², mais augmentant plus vite, et similaire à x³ mais augmentant aussi plus vite, si n est impair (cf. fig. 7 et 8).

Les fonctions polynômes sont les sommes de ces fonctions puissances, avec des coefficients : ce sont des fonctions définies par une formule du type : P(x)=c₀+c₁x+c₂x²+…+c_nxⁿ.

Les plus simples des fonctions polynômes sont les fonctions de degré 2, appelées parfois trinômes du second degré. Elles ont déjà été étudiées au lycée. Leur graphe est une parabole, comme pour la fonction x a x², mais décalée ou tournée vers le bas. En tout cas, il faut se remettre en tête toutes ces choses :

Partons d’une telle fonction, la plus générale possible, f(x)=ax²+bx+c avec a≠0 ; on peut écrire :

, avec D=b²-4ac.

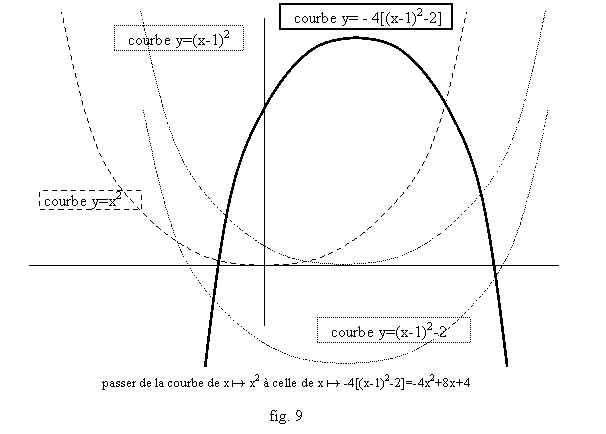
Si on pose x’=x+b/2a, on a donc f(x)=a(x’²-D/4a²). Or, pour un point donné M(x,y) du plan, remplacer x par x’ revient à changer l’origine du repère, à prendre une abscisse nulle en –b/2a, donc à déplacer l’axe des y. Autrement dit la courbe de x a x’² est la parabole habituelle, mais décalée vers la gauche ou la droite pour que son sommet coïncide avec l’abscisse –b/2a. Ensuite remplacer y par y-D/4a² revient à effectuer un décalage semblable mais vertical cette fois. Enfin multiplier par a revient à « dilater » la valeur des y (et, si a<0, on retourne le dessin par rapport à l’axe des x). Tout ceci est illustré fig. 9 et fig. 10.

Ces calculs sont souvent utilisés pour résoudre l’équation ax²+bx+c=0. Cela revient à chercher s’il existe des x pour lesquels f(x)=0, autrement dit si le graphe de f coupe l’axe horizontal. On connaît les résultats :

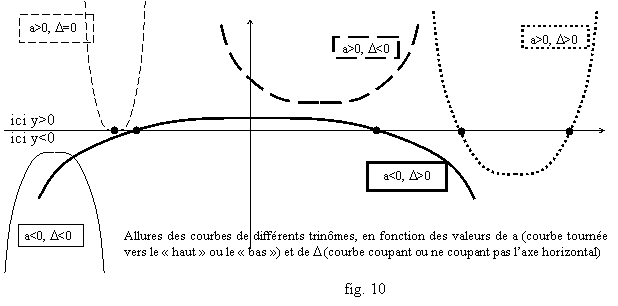
Si D<0 le trinôme ax²+bx+c est toujours du signe de a, et ne s’annule jamais (on a : ).

Si D=0, le trinôme est proportionnel à  : il est toujours du signe de a au sens large, et est l’unique solution de l’équation.

Si D>0, le nombre D/4a² est strictement positif, donc a des racines carrées, par exemple . Grâce à la formule u²-v²=(u-v)(u+v), le trinôme s’écrit :

L’équation a deux solutions, .

Les différentes allures possibles pour la courbe sont esquissées fig. 10.

Une remarque intéressante à propos de ces fonctions, sur le plan du calcul, est qu’on peut toutes les déduire de la fonction « identité », en faisant un certain nombres d’additions ou de multiplications (en utilisant éventuellement des réels). Ces idées se généralisent :

Si f et g sont deux fonctions, on peut définir :

- la somme f+g, fonction qui à un réel x fait correspondre le nombre f(x)+g(x) ;

- le produit f´g, fonction qui à un réel x fait correspondre le nombre f(x)g(x) ;

- le quotient f/g, fonction qui à un réel x fait correspondre le nombre f(x)/g(x).

On prendra garde que le domaine de définition d’une fonction obtenue par de telles opérations n’est pas R tout entier. Par exemple pour que (f/g)(x) soit défini, il faut que f(x) et g(x) soient définis, et en plus que g(x) soit non nul.

Comme application, en plus des polynômes, on peut mentionner les fractions rationnelles : une fonction f est une fraction rationnelle si on peut trouver deux polynômes P, Q tels que f(x)=P(x)/Q(x). Une telle fonction n’est pas définie partout : elle n’est pas définie quand Q(x)=0, ce qui donne une petite liste de points, et le domaine de définition est la réunion des intervalles (ouverts) entre ces points (et de deux intervalles ouverts non bornés, celui limité par le premier des points, et celui limité par le dernier).

Citons les inverses des fonctions puissances, les puissances négatives : si n est un entier naturel non nul, l’inverse 1/xⁿ de la fonction x a xⁿ est notée x a x ^-n. Toutes ces fonction ont le même domaine de définition, R^*, c’est-à-dire ]-∞,0[È]0,+∞[. Les graphes de toutes ces fonctions ont même allure sur la partie R₊^*, et aussi sur la partie R_-^*, mais la fonction est positive si n est pair (l’axe des y est un axe de symétrie) et négative si n est impair (l’origine du repère est centre de symétrie). Se reporter à la fig. 11. Sur la partie x>0, plus n est grand et plus la courbe monte « vite » en 0, et plus elle est vite collée à l’axe des x en +∞.

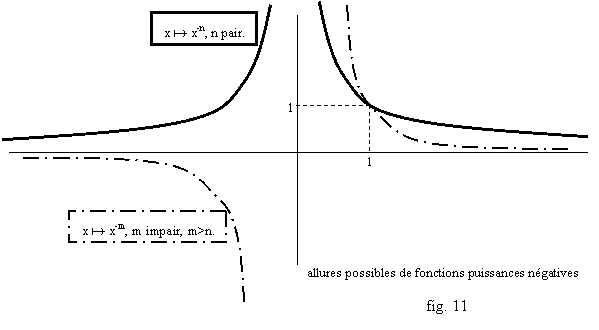
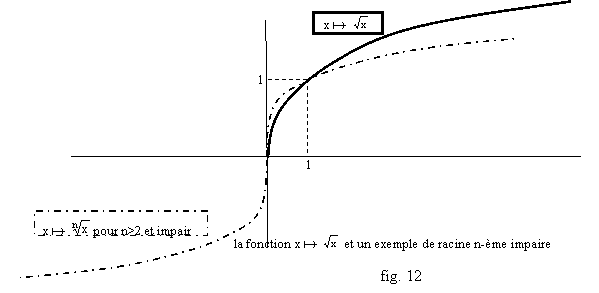
Enfin, on rappelle que les racines carrées, et autres racines n-èmes, sont des puissances. La racine carrée est notée comme la puissance 1/2, n’est définie que sur R₊, et est positive. Son graphe est représenté fig. 12. Plus généralement pour tout réel A positif et tout entier n non nul, il existe un unique réel positif t tel que tⁿ=A, on l’appelle racine n-ème de A, et on le note A^1/n. On peut ainsi définir les puissances rationnelles d’un réel A positif : si n et m sont deux entiers non nuls, A^m/n est le nombre (A^m)^1/n=(A^1/n)^m. Les graphes des fonctions racines n-èmes ont tous la même allure, de plus en plus « basse » quand n augmente (cf. fig. 12). Par ailleurs si n est impair, la racine n-ème des nombres négatifs est définie (cf. fig. 12), mais c’est un cas marginal, et on ne peut pas, en général, définir des puissances rationnels A^m/n quand A<0. Quand n est pair, les puissances n-èmes sont toujours positives dans R, donc si A<0 l’équation tⁿ=A ne peut avoir de solution. Dans ce cas, si A est positif, l’équation tⁿ=A a deux solutions opposées, A^1/n et –A^1/n.

Une autre opération très importante entre fonctions est la composition. Si f et g sont deux fonctions, on définit une nouvelle fonction nommée composée de f et g, et notée gof, de la manière suivante : pour un réel x, gof(x) sera obtenu en calculant d’abord le nombre y=f(x), puis en appliquant g à ce nouveau nombre y. On obtient gof(x)=g(y)=g[f(x)]. Cette nouvelle opération peut engendrer des problèmes ardus pour déterminer les ensembles de définitions, les valeurs de la nouvelle fonction.

Attention : l’ordre des opérations compte énormément. Ainsi posons f(x)=x+1, g(x)=x². Les fonctions f et g sont définies partout, donc gof et fog le seront aussi. Mais :

gof(x)=g(x+1)=(x+1)²=x²+2x+1.

fog(x)=f(x²)=x²+1.

On obtient deux fonctions différentes (ce qu’on peut vérifier fog(1)=2, gof(1)=4).

Autre exemple : f(x)=+1/x, g(x)=x²+1. Alors f est définie sur R₊^*, et g sur R, mais g(x) est toujours strictement positif (comme x²≥0, g(x)=x²+1≥1>0). Par conséquent si x est fixé, y=g(x)>0 donc f[g(x)]=f(y) est toujours défini. Ainsi fog est définie sur R. En revanche pour calculer gof(x) il faut commencer par calculer f(x), donc le domaine de définition de gof est un sous-ensemble de R₊^*. Encore une fois, les fonctions fog et gof sont très différentes. Dans cet exemple, on ne trouve pas d’expression très simple en faisant le calcul :

fog(x)=+1/g(x)=+1/(x²+1), et

gof(x)=f(x)²+1=[+1/x]²+1=x+2/x+1/x²+1=x+2/+1/x²+1.

Un cas fréquent est celui des composées de la fonction carrée f(x)=x² définie sur R, et de la fonction racine carrée g(x)= définie sur R₊. Par définition, g(x) est un nombre dont le carré est x, donc fog(x)=x. Mais ceci n’est vrai que quand g(x) est défini, c’est-à-dire quand x est positif. En revanche gof(x) est toujours défini puisque le nombre f(x)=x² est toujours défini et positif. Si x≥0, gof(x)==x car x est lui-même le nombre positif dont le carré vaut x². Si x≤0, c’est –x qui est le nombre positif dont le carré vaut x². Donc gof(x)= -x. On reconnaît la fonction valeur absolue. On retiendra :

Si x≥0, alors ()²=x.

Pour tout réel x, =|x|.

Les quelques courbes déjà rencontrées montrent qu’il faut pouvoir décrire l’allure générale d’une courbe avec des notions simples. La première qu’on va voir est celle qui exprime si la courbe « monte » ou « descend ».

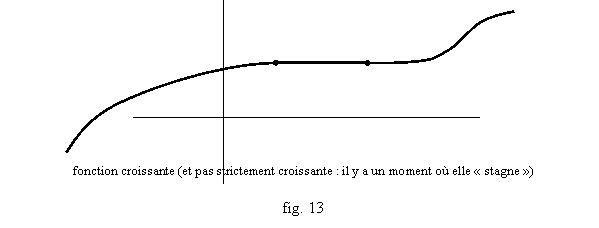
Les fonctions peuvent être monotones (« au sens large »), ou strictement monotones. Par exemple f est croissante (« au sens large », cf. fig. 13) si les images de deux nombres x, x’, sont forcément dans le même ordre (au sens large) que les nombres x,x’, c’est-à-dire si chaque fois que x>x’, on a obligatoirement f(x)≥f(x’).

Si les ordres sont toujours inversés, on dit qu’on a une fonction décroissante (fig. 14).

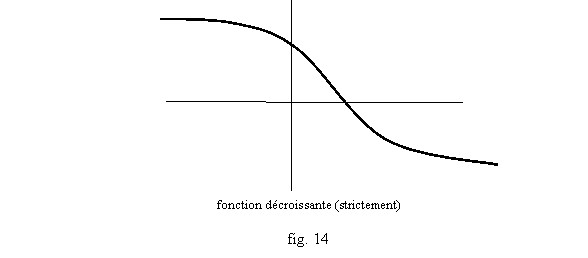
Si en plus les ordres sont conservés strictement, par exemple si f(x)>f(x’) dès que x>x’, on parle de fonction strictement croissante (cf. fig. 15 et la précision sur les fig. 13 et 14). Une fonction croissante ou décroissante est dite monotone (« au sens large »), une fonction strictement croissante ou strictement décroissante est dite strictement monotone. Avec ces définitions, une fonction constante est à la fois croissante et décroissante, mais pas strictement décroissante (ni strictement croissante). Et une fonction définie sur un intervalle est monotone mais non strictement monotone, si elle est monotone et si on peut trouver deux valeurs de x entre lesquelles la fonction reste constante (exemple sur la fig. 13).

La monotonie est donc liée à la comparaison du signe de f(y)-f(x) et du signe de y-x : si les signes sont toujours les mêmes, la fonctions est croissante, si les signes sont toujours différents, la fonction est décroissante. D’après la règle des signes, ces deux nombres ont le même signe si leur produit, ou leur quotient, est positif, et ils sont de signes opposés si leur produit, ou leur quotient, est négatif. On voit donc de nouveau réapparaître le taux d’accroissement, déjà rencontré pour les fonctions affines. On peut résumer ceci dans la règle suivante, en précisant les cas de monotonie stricte :

Soit f une fonction, x et y deux nombres distincts. On appelle taux d’accroissement de f entre x et y le nombre . Alors :

- la fonction est croissante si et seulement si tous ses taux d’accroissement sont toujours positifs ;

- la fonction est décroissante si et seulement si tous ses taux d’accroissement sont toujours négatifs ;

- la fonction est strictement croissante si et seulement si tous ses taux d’accroissement sont toujours strictement positifs (cf. fig. 15 : si on prend une droite qui coupe la courbe en deux points, elle « monte », ce qui correspond bien à une pente positive, et la pente de la droite passant par deux points M_x(x,f(x)) et M_y(y,f(y)) de la courbe est justement le taux d’accroissement) ;

- la fonction est strictement décroissante si et seulement si les taux d’accroissement sont toujours strictement négatifs ;

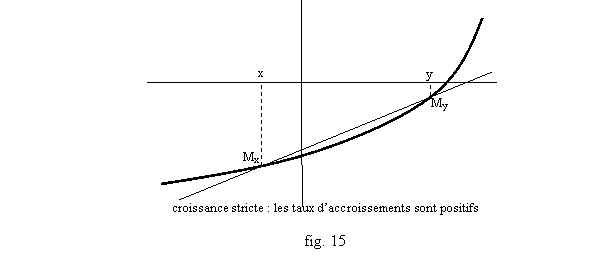
Ce taux d’accroissement n’est pas toujours difficile à calculer. À titre d’exemple, on peut prouver, ce qu’on a déjà représenté en fig. 7 et 8 : si n est un entier positif, la fonction x a xⁿ est croissante strictement sur R₊. On en profitera pour écrire une égalité importante, qui rend de fréquents services, et généralise l’identité remarquable a²-b²=(a-b)(a+b).

Identité remarquable : si a,b sont deux réels, on a :

aⁿ-bⁿ=(a-b)(a^n-1+a^n-2b+a^n-3b²+…+b^n-1)=(a-b)

Développons le produit (a-b) : on trouve a-b. Or on a :

a et

-b.

Dans la deuxième somme, on remarque qu’intervient le nombre k+1, avec k allant de 0 à n-1. Il revient au même de considérer le nombre j=k+1, qui variera de 0+1=1=(n-1)+1=n. On peut reprendre la lettre k après :

-b.

Finalement on a :

a-b=.

On a deux sommes d’expressions identiques, l’une commençant à 0 et finissant à n-1, l’autre commençant à 1 et finissant à n. La somme commune, de 1 à n-1, s’élimine donc, et il reste : a^n-0b⁰-a^n-nbⁿ=aⁿ-bⁿ. Finalement on a bien obtenu l’égalité :

(a-b)=aⁿ-bⁿ.

Si x,y sont deux réels positifs et distincts, on peut leur appliquer cette égalité :

(y-x)=yⁿ-xⁿ

donc on a l’expression du taux d’accroissement :

=

Cette somme de nombres tous positifs (car x et y sont positifs) est positive, donc on a déjà la preuve que la fonction puissance n est croissante. Par ailleurs si les deux nombres sont distincts et positifs, l’un des deux au moins est non nul, par exemple x. Dans ce cas x^n-1 est non nul aussi, et comme la somme est égale à x^n-1>0, plus d’autres termes positifs, elle est strictement positive. On a donc bien prouvé que les taux d’accroissement sont strictement positifs.

Une dernière notion relative au sens de variation, qui est apparente par exemple sur les graphes des fonctions comme x a x² est la notion d’extremum.

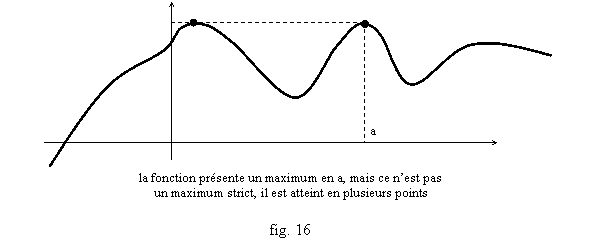
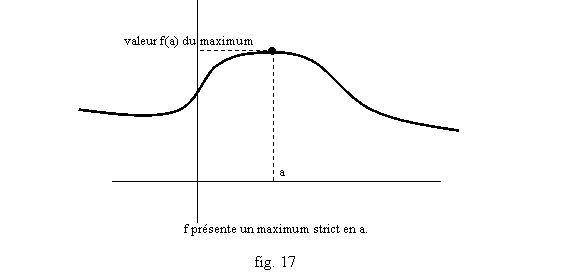
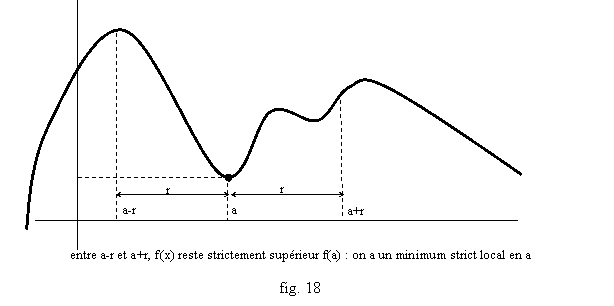
Soit f une fonction et a un nombre. On dit que f présente un maximum (« au sens large ») en a si f(x)≤f(a) pour tout x (fig. 16). On dit que f présente un maximum strict en a si f(x)<f(a) pour tout x différent de a (fig. 17). On définit de même un minimum (« au sens large »), un minimum strict. Si f présente un maximum ou un minimum, on dit qu’elle présente un extremum au sens large en a, et si c’est un maximum ou un minimum strict, on parle d’extremum strict. Enfin on dit que f présente un maximum local en a si on peut isoler un intervalle autour de a, qui peut s’écrire par exemple ]a-r,a+r[ avec un réel r>0, telle que f(x)≤f(a) si x est entre a-r et a+r. On définit de même un maximum local strict, minimum local, minimum local strict (fig. 18), extremum local, extremum local strict.

Pour les taux d’accroissements, la notion d’extremum en a correspond à ce que les taux d’accroissement entre x et a sont tous d’un même signe quand x<a, et tous du signe opposé quand x>a (puisque les différences f(x)-f(a) ne changent pas de signe, f(a) étant plus petit que tous les f(x), ou plus grand que tous, alors que x-a est négatif si x<a et positif si x>a).

Pour finir sur ces considérations sur les fonctions, on va aussi rappeler la généralisation classique des symétries possibles sur les courbes des fonctions, déjà constatées sur les cas simples (fonctions puissances, fig. 7, 8, 11, valeur absolue, etc.).

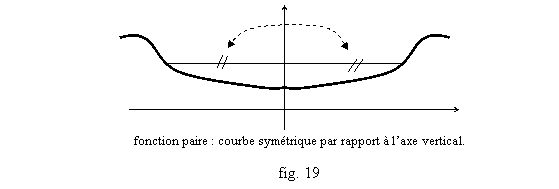
- Une fonction f est une fonction paire (comme x a xⁿ avec n pair), si pour tout x, f(-x)=f(x). Le graphe de f a alors un axe de symétrie : l’axe vertical du repère (fig. 19).

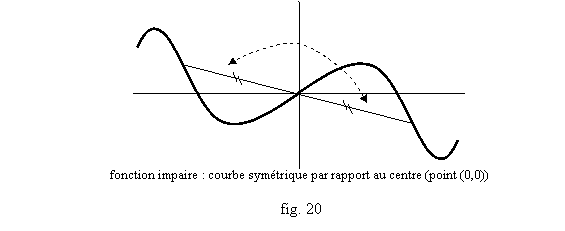
- Une fonction f est impaire (comme x a xⁿ avec n impair) si pour tout x, on a l’égalité : f(-x)= -f(x). Le graphe de f a alors un centre de symétrie : l’origine du repère (fig. 20).

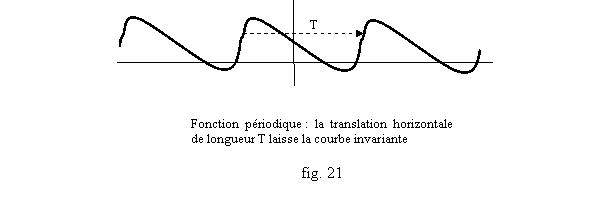
- Soit une fonction f, et T un réel strictement positif. On dit que f est périodique de période T si pour tout x on a f(x+T)=f(x). Le graphe de f est alors invariant quand on lui fait subir une translation horizontale de longueur T (et donc aussi par des translations horizontales de mesures 2T, 3T, -T, -2T, …) (fig. 21).

- On verra plus tard d’autres symétries possibles.

Exercices :

1) Résoudre dans R les équations suivantes : x²+x+1=0 ; 3x²+2x+1=0 ; x³+2x²-6x=0 ; x⁴-x²-1=0.

2) Même question pour les équations suivantes : x+1/x=2 ;  ; 1/(x+1)=1/x+1.

3) Démontrer les inégalités suivantes, vraies pour toute paire de réels positifs x,y :

-  ;

-  ;

- x+1/x≥2.

4) On se donne deux fonctions croissantes f,g. Montrer que la somme f+g est croissante. Montrer que, si f et g sont positive, le produit f´g est croissant. On pose f(x)= -1/x, g(x)=x². Montrer que f et g sont croissantes strictement sur R₊^*, mais que f´g est strictement décroissante sur cet intervalle.

5) Pour chacune des fonctions suivantes, vérifier que le taux d’accroissement T entre deux réels distincts x et y est donné par l’expression proposée :

- Pour f(x)=1/x, T= -1/(xy) ;

- Pour ,  ;

- Pour ,  ;

- Pouvez-vous généraliser les deux précédents calculs au cas de  ?

6) On se donne deux fonctions f,g et deux réels distincts x,y, et on note T_f et T_g les taux d’accroissements pour f et pour g entre x et y. Montrer que :

- Pour f+g, le taux d’accroissement entre x et y est T_f+T_g ;

- Pour fg, c’est f(y)T_g+g(x)T_f ;

- Pour f/g, c’est [g(x)T_f-f(y)T_g]/[g(x)g(y)].

7) Etudier le sens de variation des fonctions suivantes : f(x)=x³+x²+1 sur R₊ ; f(x)=1/x-1/(x+1) ; f(x)=.

8) Etudier les ensembles de définition des fonctions suivantes : f(x)= ; f(x)= ; f(x)= ; f(x)= ; f(x)=.

9) Exprimer le plus simplement possible les composées de fonctions suivantes, en mettant les polynômes sous forme développée :

- fog et gof avec f(x)=x³, g(x)=2-x ;

- fof, fo(fof), fo[fo(fof)], avec f(x)=1/(x+1) ;

- fog et gof pour g(x)=E(x), f(x)=x-E(x).

10) Soit G une fonction telle que, pour toute f, on ait Gof=f ; montrer que G est la fonction identité (on utilisera l’hypothèse en prenant pour f des fonctions constantes).

11) Soit G une fonction telle que, pour toute f, on ait Gof=foG. Montrer que G est l’identité.

12) Soit G une fonction telle que, pour tout f, on ait Gof=G. Montrer que G est constante.

13) Si f(x)=ax+b et g(x)=a’x+b’ sont deux fonctions affines, montrer que fog est affine et calculer sa pente et son ordonnée à l’origine en fonction de a,a’,b,b’.

14) Trouver toutes les fonctions affines f telles que fof=Id (utiliser l’exercice 13). Existe-t-il d’autres fonctions vérifiant fof=Id que les fonctions affines trouvées ?

15) Montrer que pour tout entier p et tout réel x, on a E(x+p)=E(x)+p.

16) Soit f(x)=ax+b une fonction affine telle que Eof=foE (*), où E est la fonction partie entière.

- a- Montrer que a et b sont forcément des entiers (utiliser l’égalité (*) pour des valeurs particulières, par exemple 0) ;

- Montrer que a=1. En déduire que les seules fonctions affines vérifiant (*) correspondent à l’égalité de l’exercice 16.

17) La fonction f(x)=1/x est-elle monotone sur R₊^* ? sur R_-^* ? sur R^* ?

18) Les fonctions suivantes sont-elles paires ou impaires ? f(x)=x³+x ; f(x)=x³+x+1 ; f(x)=C (constante) ; f=Id ; f(x)=E(x) ; f(x)=(x-E(x)-1/2)² ? Montrer que la dernière de ces fonctions est périodique.

19) Etudier la parité d’une composée fog, en fonction de la parité de f et de g (on suppose que chacune des deux est paire, ou impaire).

20) Que dire d’une fonction à la fois paire et impaire ?

21) Définir trois fonctions distinctes f,g,h, définies sur R tout entier, et telles que, pour tout réel x, on ait :

|f(x)|=|g(x)|=|h(x)|=2.

3) Limites des fonctions. Continuité en un point.

Pour étudier, pour une fonction donnée, la façon dont les valeurs f(x) varient quand x varie, on va d’abord regarder si cette variation se fait de manière « régulière » ; en particulier, on se restreindra aux fonctions dont les valeurs ne font pas de « sauts », comme par exemple la fonction partie entière, qui passe de la valeur 0 quand x<1, à la valeur 1 en x=1 (il y a un tel saut à chaque fois que x est entier, cf. paragraphe 2, fig. 6). Ceci correspond aux notions de fonction continue et de limite d’une fonction en un point x.

On dit que la fonction f(x) a pour limite le nombre l quand x tend vers le nombre x₀, si la valeur f(x) peut être rendue aussi proche de l qu’on le veut, du moment que x est assez proche de x₀ (fig. 1). (Cela se définit ainsi : quel que soit le réel e>0, on peut trouver un intervalle I_r=]x₀-r,x₀+r[ autour de x₀, avec r>0, tel que si xÎI_r, on ait f(x)Î]l-e,l+e[ ; on n’a pas besoin de comprendre ou de savoir utiliser une telle définition pour le moment).

On notera cette propriété : .

Cette notion sera définie rigoureusement au 2^ème semestre en analyse. Pour l’instant il importe surtout de savoir calculer avec. Pour ce faire on a les règles suivantes :

Si f(x) et g(x) ont pour limites les nombres l et l’ quand x tend vers x₀, alors la fonction somme, x a f(x)+g(x), tend vers l+l’ quand x tend vers x₀, la fonction produit x a f(x)×g(x) tend vers l×l’ quand x tend vers x₀, et si l’≠0, la fonction quotient x a f(x)/g(x) est définie au moins dans un petit intervalle autour de x₀ et tend vers l/l’.

On définit aussi les limites en ±∞, et les limites infinies.

Si f(x) devient aussi grand qu’on veut du moment que x est assez proche de x₀, on dit que f(x) tend vers +∞ en x₀ (fig. 2 ; la définition rigoureuse est : quel que soit le réel A, on peut trouver un intervalle I_r=]x₀-r,x₀+r[ autour de x₀, avec r>0, tel que si xÎI_r on ait f(x)>A). On a une notion analogue pour la limite -∞, et on sait que beaucoup d’opérations fonctionnent avec ces limites : par exemple +∞+l=+∞, (+∞)×(-∞)=-∞, etc. Les opérations 0×∞, 0/0, ∞-∞, ∞/∞, etc., sont des « formes indéterminées », il faut étudier la fonction plus en détail pour pouvoir conclure quand une limite semble se présenter sous cette forme.

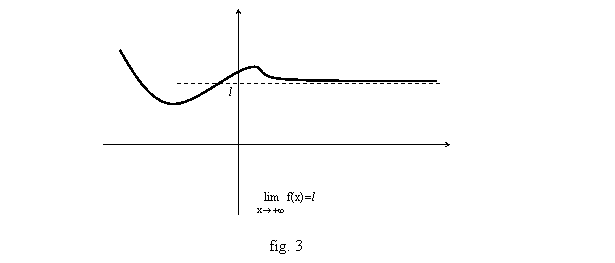
Enfin si f(x) peut se rapprocher aussi près qu’on veut d’une limite du moment que x devient assez grand, on parle de limite quand x tend vers +∞ (fig. 3 ; définition : quel que soit e>0, on peut trouver A tel que, si x>A, f(x)Î]l-e,l+e[ ; cette limite peut aussi être elle-même égale à ±∞).

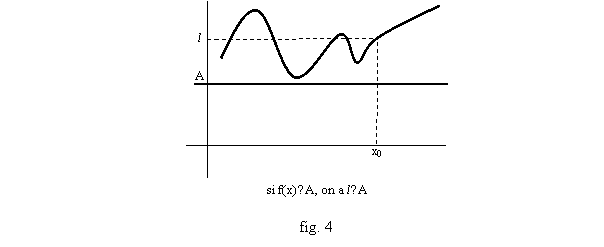
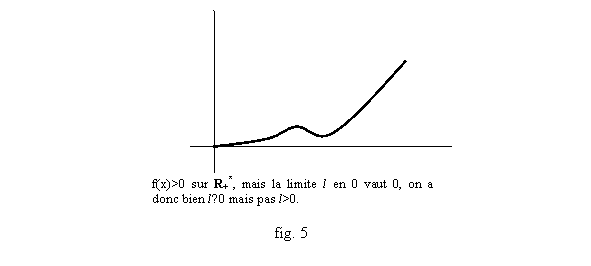
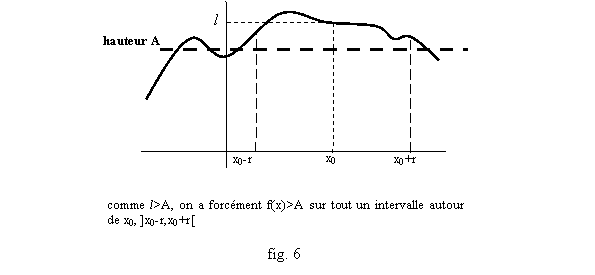
Il faut retenir la « régularité » du « passage à la limite » avec l’ordre : si une fonction f a une limite l (l peut être ici infinie) quand x tend vers x₀, et si on a une inégalité du type f(x)≥A ou f(x)>A au moins dans un intervalle qui jouxte x₀ (comme ]a,x₀[, ou ]x₀,b[, pour un a<x₀ ou un b>x₀), alors la limite l vérifie l≥A (fig. 4) (de même avec une inégalité du type f(x)≤B, on aura l≤B). Attention : on n’obtient qu’une inégalité large. On peut avoir f(x)>l sur tout un intervalle ]a,x₀[, et avoir néanmoins l comme limite. Par exemple les fonctions x², |x|, sont >0 sur R^*, mais ont pour limite 0 en 0 (fig. 5). En revanche, si on connaît la limite l d’une fonction en x₀, et qu’on a une inégalité stricte l>A (ou respectivement l<A) entre l et un autre réel A, on aura forcément un intervalle autour de x₀, du type ]x₀-r, x₀+r[ avec r>0, sur lequel on ait f(x)>A (respectivement f(x)<A ; cf. fig. 6).

On retiendra de toute façon qu’on peut « passer à la limite » dans les inégalités, c’est-à-dire qu’une inégalité du type f(x)≤g(x) entraînera lim f ≤ lim g (en prenant la limite en un même point x₀). Mais on obtient toujours des inégalités larges pour les limites, ≥ ou ≤, jamais d’inégalités strictes.

On peut aussi « composer les limites » : on sait que quand x a f(x) et y a g(y) sont deux fonctions, telles que f(x) soit toujours dans l’ensemble de définition de g, on peut définir la composée de f et g, gof. Alors si f(x) tend vers une limite l₀ quand x tend vers x₀, et si par ailleurs g(y) tend vers une limite L quand la variable y tend vers le nombre l₀, alors gof(x) tend vers L quand x tend vers x₀. On fera toujours très attention aux ensembles de définition avant d’utiliser cette règle.

La dernière règle pour découvrir la limite d’une fonction, est le célèbre théorème des gendarmes :

Théorème des Gendarmes : (fig. 7) si f, g₁, g₂ sont trois fonctions telles que g₁(x)≤f(x)≤g₂(x), et si g₁ et g₂ ont une même limite L quand x tend vers x₀, alors f(x) tend vers L quand x tend vers x₀.

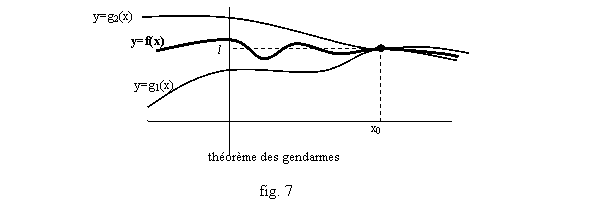
C’est ce théorème qui permet de résoudre de nombreux calculs de limites, une fois admises certaines limites de références, qu’on donne ci-dessous :

- une fonction constante de valeur C a pour limite C en tout point x₀.

- La fonction identité a pour limite x₀ en tout point x₀ ;

- Si p est rationnel, la fonction puissance x^p a pour limite (x₀)^p en tout point x₀ ; ainsi tend vers quand x tend vers x₀, quel que soit le réel x₀≥0 fixé.

Il faut se familiariser avec ces techniques de calcul de limites : souvent, il suffit de substituer x₀ à la variable – ou bien les certaines limites déjà connues, et on effectue le calcul en faisant bien attention aux formes indéterminées, qui obligent à tout reprendre, à transformer l’expression de la fonction avant de pouvoir conclure.

Exemple 1 : calculer la limite .

La fonction étant une fraction rationnelle (quotient de polynômes), est continue là où elle est définie. En x=1, le dénominateur vaut 1-1²+2.1=2≠0, donc la fraction est définie en x=1, et la limite est égale à la valeur, en x=1, c’est-à-dire : .

Exemple 2 : calculer la limite .

La fonction étant une fraction rationnelle (quotient de polynôme), est continue là où elle est définie. En x=1, le dénominateur vaut 1+1²-2.1=0, donc la fraction n’est pas définie en x=1 : elle se présente sous la forme 4/0, et a donc une limite infinie en valeur absolue quand x tend vers 1. Le dénominateur et le numérateur, qui s’écrivent (1-x)² et (1+x)², sont positifs. Le quotient d’une fonction positive qui a une limite non nulle par une fonction strictement positive qui tend vers 0, tend vers +∞, on a donc : .

Exemple 3 : calculer la limite .

Dénominateur et numérateur sont des fonctions continues de x, qui, à la limite, se présentent sous la forme 1×0 et 0×2 respectivement. Bien sûr, on ne peut pas simplifier par 0, c’est donc la forme indéterminée 0/0. Il faut donc modifier l’expression de la fonction pour pouvoir trouver la limite. Avec les sommes et différences de racines carrées, une technique possible est l’utilisation des quantités conjuguées : . On peut donc transformer la fonction grâce à ce calcul :

et sous cette forme, on a levé l’indétermination, puisque le dénominateur tend vers et le numérateur vers 1+1=2. La limite existe donc et vaut : 2/2=1.

On s’entraînera aussi à calculer des limites en ±∞ (souvent il suffit d’utiliser les limites connues, comme 1/x qui tend vers 0 quand x tend vers ±∞ : on remplace alors ces expressions par 0).

La notion de limite sert à préciser quelle fonction est assez régulière pour obéir à des propriétés intéressantes dans les calculs, et quelle fonction ne l’est pas. On étudiera en fait le plus souvent les fonctions continues :

Définition : (cf. fig. 8) une fonction est continue en un point x₀ si f(x) a pour limite f(x₀) quand x tend vers x₀. Une fonction est continue sur un intervalle I si elle est continue en tout point de I.

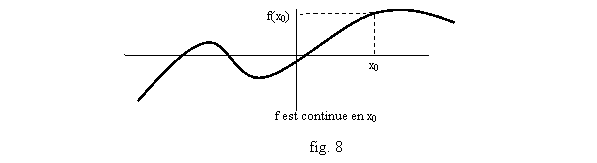
Exemple : d’après les limites de référence, les fonctions constantes, la fonction identité, sont continues. En revanche la fonction partie entière n’est pas continue : en x₀=1 par exemple, E(x) garde la valeur 0 à gauche de 1 (quand x<1) et la valeur 1 à droite de 1. On dit qu’il y a une limite à gauche et à droite (égales à 0 et 1 respectivement), mais comme ces deux limites ne sont pas égales, il n’y a pas de limite, et la fonction n’est pas continue (on dit qu’elle est continue à droite, puisque la limite à droite est 1=E(1), mais discontinue à gauche). Autre exemple fig. 9 (on note x ® x₀⁺ pour les limites à droite, x ® x₀^- pour les limites à gauche).

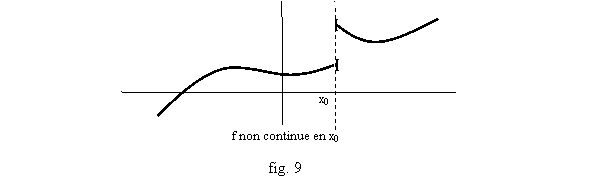
Il y a aussi des fonctions n’ayant pas de limite du tout, ni à gauche ni à droite, comme la fonction égale à 1/x-E(1/x) (partie décimale de 1/x) sur R^*, et valant 0 quand x=0. On s’en rendra compte en la faisant tracer par ordinateur ou calculatrice (ou en regardant fig. 10).

Comme 1/x-E(1/x) prend des valeurs proches de 0 et aussi proches de 1 quand x se rapproche de 0, elle n’a aucune limite en 0. Ce type de problème est en fait assez rare quand on se limite à des fonctions simples, comme on en rencontre dans les exercices ou dans les applications des mathématiques aux différentes sciences qui les utilisent. En revanche, des fonctions comme E(x) ou comme la fonction représentée en fig. 9 présentent un aspect plus courant : il y a certains points ou la fonction est continue (la plupart), mais certains endroits particuliers aussi où elle ne l’est pas (les points entiers …,-2,-1,0,1,2,3,… pour la fonction partie entière, le point x₀ représenté pour la fonction de la fig. 9).

La fonction valeur absolue est continue : elle est continue en tout x₀≠0, car elle est égale à x ou à –x dans tout un intervalle autour de x₀. Et en 0, elle a pour limite 0 à gauche (elle vaut x) et à droite (elle vaut –x qui tend vers -0=0). Donc elle est aussi continue en 0.

Néanmoins il y a beaucoup de fonctions continues. Les propriétés rappelées sur les limites ont des conséquences immédiates :

Une somme, un produit de fonctions continues, est continu, ainsi qu’un quotient de fonctions continues, sur tout intervalle où il est défini. Conséquence : toute puissance positive, qui se déduit de l’identité par des produits, est continue, tout polynôme, qui se déduit des puissances et des constantes par multiplications et additions, est continue, ainsi que les fractions rationnelles là où elles sont définies.

Une composée gof de fonctions continues est continue (en supposant qu’elle soit définie). Conséquences : les fonctions comme |P(x)| avec P polynôme, sont continues.

Exercices :

1) Pour les fonctions suivantes, trouver les points où elles sont définies, ceux où elles sont continues, et ceux où elles ne sont pas continues : f(x)=E(x) ; f(x)=x-E(x) ; f(x)=1/(x-E(x)) ; f(x)=(x-E(x)-1/2))².

2) Etudier si les limites suivantes existent, et si oui les calculer :  ;  ;  ; .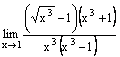

3) Mêmes questions pour les limites suivantes : avec n,m entiers, n,m>1, (on discutera suivant les valeurs de n et m) ; , mêmes conditions pour n et m ; , n et m entiers, n,m>0 ;  ; .

4) Montrer que .

5) Soit f une fonction, telle que f(x) tend ver l quand x tend vers x₀. Montrer que si l n’est pas entier, Eof(x) tend vers E(l) quand x tend vers x₀. Que se passe-t-il si l est entier ?

4) Fonctions continues sur un intervalle.

Les fonctions continues sur un intervalle ont des propriétés importantes, qui viennent de ce que les fonctions continues, par leur définition, sont celles dont la courbe « n’a pas d’à-coups », est « d’un seul tenant », peut se dessiner « sans lever le crayon ».

La première propriété est la propriété (ou le théorème) des valeurs intermédiaires (fig. 1) :

Théorème des valeurs intermédiaires : Si f est une fonction définie sur un intervalle [a,b] et continue, alors tout nombre compris entre f(a) et f(b) est atteint au moins une fois entre a et b (autrement dit si Y est un réel qui est entre f(a) et f(b), alors l’équation f(x)=Y a au moins une solution dans l’intervalle [a,b]).

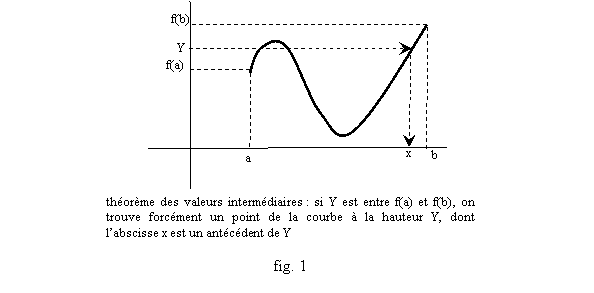
Dans une telle situation, l’ensemble de toutes les valeurs prises par f entre a et b (l’ensemble de tous les nombres f(x) quand x est rendu égal à tous les nombres possibles entre a et b), s’appelle l’image par f de l’intervalle [a,b], et se note f([a,b]). Quand y est un élément de cet ensemble, un nombre x tel que f(x)=y s’appelle antécédent de y. Une conséquence du théorème des valeurs intermédiaires est la propriété suivante :

Si f est une fonction continue sur un intervalle I, alors f(I) est un intervalle (attention : ce n’est pas forcément un intervalle de même nature, ouvert, fermé, etc.)

En effet on a dit que les intervalles sont les sous-ensembles « sans trous » de R, et le théorème des valeurs intermédiaires dit justement que si f est continue et si x parcourt toutes les valeurs d’un intervalle I, alors il n’y a pas de « trou » dans les valeurs prises par f(x), donc ces valeurs forment un intervalle.

Propriété cruciale : si I est un intervalle fermé borné, et f continue, alors l’image par f de I est aussi un intervalle fermé borné (fig. 2).

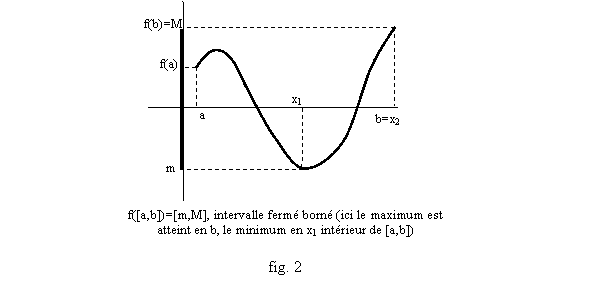
Théorème : Si I=[a,b] est un intervalle fermé borné et f une fonction continue, alors l’image f(I) est un intervalle fermé borné [m,M], c’est-à-dire qu’on peut trouver deux nombres m et M tels que :

§ m est une valeur prise par f, on peut donc lui trouver un antécédent x₁ entre a et b tel que f(x₁)=m, et c’est la plus petite valeur prise entre a et b, c’est-à-dire que f(x)≥m pour tous les réels x entre a et b (on dit que m est le minimum de f(x) sur [a,b], atteint en x=x₁) ;

§ M est une valeur prise par f, on peut donc lui trouver un antécédent x₂ entre a et b tel que f(x₂)=M, et c’est la plus grande valeur prise entre a et b, c’est-à-dire que f(x)≤M pour tous les réels x entre a et b (on dit que M est le maximum de f(x) sur [a,b], atteint en x=x₂) ;

§ Tous les nombres y entre m et M ont au moins un antécédent x, tel que f(x)=y, entre a et b.

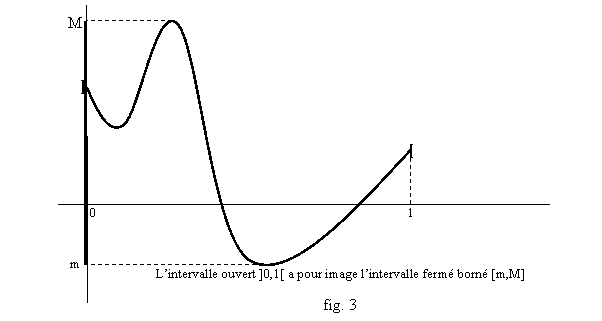
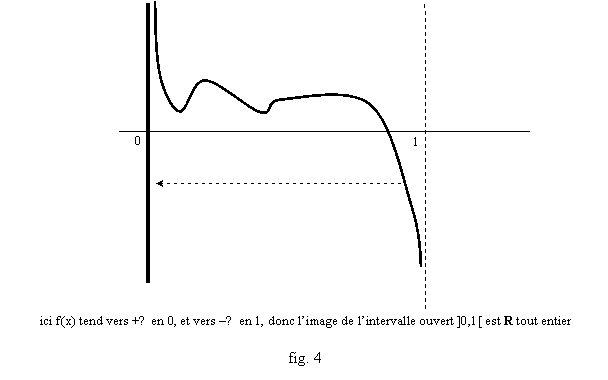
Tout ce qui n’est pas dit dans ce théorème peut être faux : ce n’est pas forcément en a ou en b que les valeurs m et M sont atteintes, et ils peuvent aussi avoir plusieurs antécédents ; par ailleurs si I n’est pas un intervalle fermé borné on peut quand même avoir une image f(I) fermée bornée (cf. fig. 3), ou avoir en fait n’importe quel type d’intervalle (exemple fig.4, exercices 12 à 14) et si f n’est pas continue on ne peut rien dire du tout. Par exemple, par la fonction partie entière, l’image de n’importe quel intervalle de longueur plus grande que 1 est une suite (finie ou infini, comme l’intervalle) de nombres entiers, isolés les uns des autres.

Les théorèmes sur les fonctions continues servent pour prouver d’autres résultats théoriques. Dans les exercices, on se servira souvent du théorème des valeurs intermédiaires pour prouver l’existence de solutions à certaines équations. Souvent les équations se présentent sous la forme F(x)=0, et on est sûr qu’une telle équation a une solution entre deux nombres a et b si F(a) et F(b) sont de signes différents. On formule parfois le théorème des valeurs intermédiaires sous cette forme : « une fonction continue ne peut pas changer de signe sans s’annuler ».

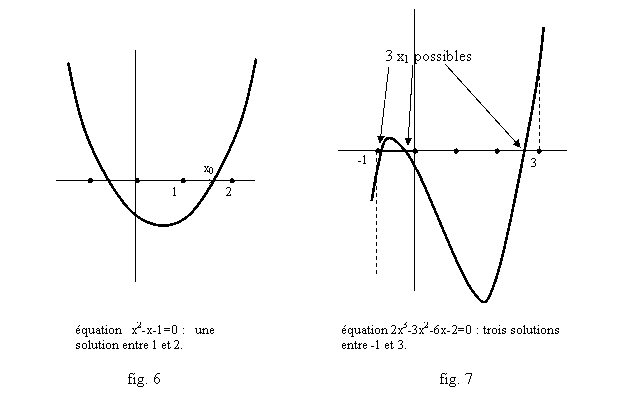
Exemple : montrer (sans utiliser D) que l’équation x²-x-1=0 a une solution x₀ telle que 1<x₀<2, et que l’équation 2x³-3x²-6x-2=0 a une solution x₁ telle que -1<x₁<3.

On pose f(x)=x²-x-1 et g(x)=2x³-3x²-6x-2. Ce sont deux polynômes donc deux fonctions continues ; on a f(1)= -1, f(2)=1, g(-1)= -1, g(3)=7. On a donc f(1)<0<f(2), et g(-1)<0<g(3), le théorème des valeurs intermédiaires permet de conclure : il existe forcément un x₀ entre 1 et 2 et un x₁ entre -1 et 3, tels que f(x₀)=0 et g(x₁)=0.

Le théorème prouve l’existence des solutions, mais ne donne aucun moyen de les calculer, ni même de savoir combien il y en a. On voit sur les figures 6 et 7 que dans un cas, il y a une seule solution (c’est le « nombre d’or », tel que x²=x+1), mais dans l’autre il y en a en fait trois (on a donné l’allure approximative de la courbe). On peut résoudre cette difficulté si on connaît le sens de variation exact d’une fonction sur un intervalle. En effet une fonction f strictement croissante par exemple, ne peut avoir qu’une solution à l’équation f(x)=0, puisque si x₀ est cette solution, les x<x₀ vérifieront f(x)<f(x₀)=0 et les x>x₀ vérifieront f(x)>f(x₀)=0. Par exemple pour g, si on découpe R en trois intervalles avec g strictement croissante sur le premier et le troisième (cf. fig. 7), et strictement décroissante sur le deuxième, on pourra dire qu’il y a au maximum une solution à l’équation g(x)=0 sur chacun, et ainsi prouver qu’il y a 3 solutions en tout.

Il faut donc pouvoir découvrir les sens de variations des fonctions, c’est un des objets du prochain chapitre.

Exercice :

1) Montrer que les équations suivantes ont au moins une solution sur l’intervalle ]0,1[ (on ne demande pas de calculer de solution) : x³-3x+1=0 ; 4/(x+1)+x²-5=0 ; 1/x-4x²+1=0 ; x⁴+x³-5x²+x=0 ; 1/x+1/(x-1)+1=0.

2) Montrer que les équations suivantes ont une solution sur l’intervalle indiqué : x³+x=1 sur [0,1] ; x³+4x=x²+2 sur [0,1] ; x⁴+x=10 sur [1,2] ; x⁶+x²-1=0 sur [-1,1].

3) Mêmes questions dans les cas suivants : x+1/x=11 sur [1,+∞[ ; sur R₊^*.

4) On pose f(x)=1/x+x. On a f(1)=2, f(-1)=-2. Montrer que l’équation f(x)=0 n’a aucune solution dans R. Cela contredit-il le théorème des valeurs intermédiaires ? Expliquer.

5) Soit f une fonction continue définie sur [0,1], telle que pour tout x on ait f(x)Î[0,1]. Montrer qu’il existe un élément x₀ de [0,1] tel que f(x₀)=x₀.

6) Soit f, g deux fonctions continues définies sur [0,1] telles que : a) pour tout x on ait f(x)Î[0,1] ; b) on a g(0)≤0, g(1)≥1. Montrer qu’il existe un x₀Î[0,1] tel que g(x₀)=f(x₀).

7) Soit f, g deux fonctions continues définies sur [0,1] telles que : a) pour tout x on ait f(x)Î[0,1] ; b) tout yÎ[0,1] a un antécédent x par g dans [0,1] (on peut trouver xÎ[0,1] tel que g(x)=y). Montrer qu’il existe un x₀Î[0,1] tel que g(x₀)=f(x₀).

8) Soit f une fonction continue sur R et périodique. Montrer que f(R), l’image de R tout entier (l’ensemble de tous les f(x) quand x parcourt R), est un intervalle fermé borné.

9) On pose si x¹0, et f(0)=0. f est-elle continue sur R ? déterminer f(R).

10) Mêmes questions avec .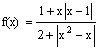

11) On pose F(x)=4|x-E(x)-1/2|-1. Montrer que F est continue, périodique, et qu’on a : F(R)=[-1,1].

12) On garde la notation F pour la fonction étudiée au 11). On pose g(x)=F(1/x) si x¹0, g(0)=0. Montrer (qualitativement, on ne cherchera pas à faire une preuve détaillée) que g n’est pas continue, mais que l’image de n’importe quel intervalle par g est un intervalle. En particulier montrer que g(I)=[0,1] pour tout intervalle contenant 0 (« vrai », pas réduit à un point [0,0]).

13) On garde la notation g pour la fonction étudiée au 12. On pose pour x>0, f(x)=g(x)/x. Justifier que f est continue et que pour tout a>0, l’image f(]0,a]) est égale à R tout entier (on pourra se contenter d’un dessin soigné).

14) En s’inspirant des exercices précédents, montrer (qualitativement, par un dessin par exemple) qu’on peut trouver 9 fonctions continues, définies sur ]0,1], telles que les images de ]0,1] par ces fonctions soient des intervalles des 9 types différents (ouvert borné, fermé borné, semi-ouvert à gauche, etc.).